図形数学証明の結果 ~ Josspixtfye

検索キーワード「図形数学証明」に一致する投稿を日付順に表示しています。関連性の高い順すべての投稿を表示

いろいろ中学二年数学証明 215262-中学二年数学証�� コツ

Studydoctor作図の証明中２数学 Studydoctor

数学の証明問題を攻略するための6つのコツつぎの例題をときながら解説するよ。 AB = DC、AB // DCの ABCと CDAがあったとします。このとき、角ABC = 角CDAであることを証明し動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

中学二年数学証明コツ

√70以上図形公式中学覚え方 230759-図形公式中学覚え方

中学生公式確認問題①図形編解答 ①円の面積の公式： πr² （半径をr、円周率をπ）半径×半径×314などもOKです！小学校でも習う円の面積。これを間違ってしまった方は、大ピンチです！！！ ②円周の長さの公式： 2πr

【ベストコレクション】中学 2 年数学確率 281509

前ちゃんの中学校数学の部屋：パワーポイント補助教材2年教材のダウンロードプレゼンテーション教材 2年この教材を使用した授業方法は、こちらをご参考にしてください。ダウンロードに関する注意事項ダウンロードの前にお読みください今回は、「確率の求め方」を学習するよ。コインを投げたり、サイコロを投げたりと、すでに何度か確率を求めてきたね。こうした確率の求め方を公式にすると、次のようになるよ。以上より、Bが当たる確率はこのようになります。くじを元に戻さないパターンでは、2回目にくじを引くとき、はずれと当たりがそれぞれ何本ずつ残っているのかを考えることが大事ですね！更に、注目してほしいのは 1回目にくじを引いて当たりを

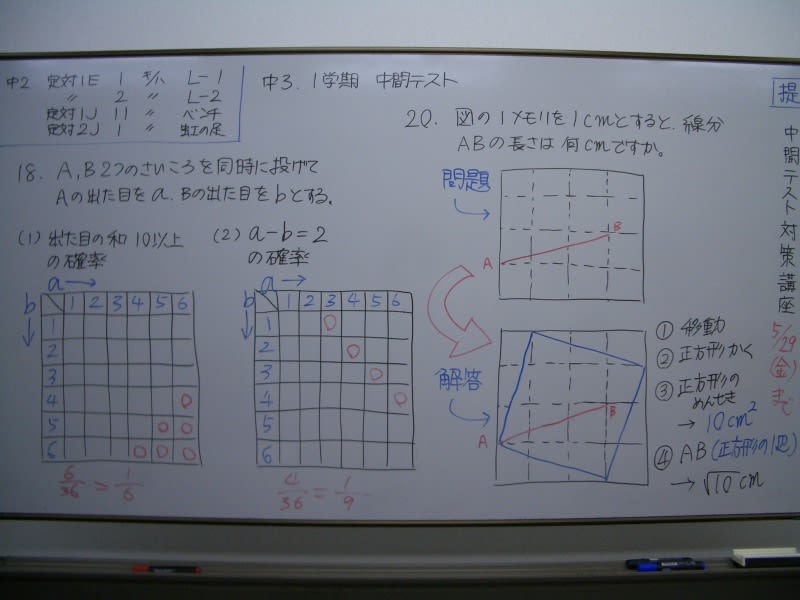
中3数学中間テストは確率と平方根ブログアビット

中学 2 年数学確率

√無料でダウンロード！円錐高さ求め方中学 264426-円錐高さ求め方中学

（中学2年の中点の座標，直線の方程式も使う）三角形の面積の二等分線（底辺）×（高さ）÷2 で求められます。次のように分数の形で書くこともできます。（面積）＝図1 (1) 2で割ることを忘れる答案が多いので注意しましょう。次図2の三角形の面積は、 4 × 3=12 ではなく、 4 × 3 ÷ 2=6 に257 = 32 25 7 = 32 （㉜）が、 96−21× 2 = 54(cm) 96 − 21 × 2 = 54 ( c m) です。 54cm 54 c m を 25 7 25 7 に比例配分します。 54× 7 257 = ×1 16 (cm) 54 × 7 25 7 = × 1 16 ( c m) これが、求める小さい球の半径です。あとは、これを小学生、中学生に分るように、ちょいと丁寧に説明すれば済むだろう。実際に模型を作るのも間単だ。さて、ここで、三角形の場合と比べてみよう。三角形の面積は底（底辺の長さ）×高さを2で割るので、2が出てくる。ということは、底

緊急ですこの円錐の下の円の半径と円錐台の高さの求め方を教えて下さい Yahoo 知恵袋

円錐高さ求め方中学

√ 正四角錐表面積 339356-正四角錐表面積求め方

面積 = 16×11÷2= これが2つあるので ×2=176 底辺=8cm, 高さ=13cmのものは面積 = 8×13÷2= 52で，abcd と比べると面積は 2 1 である。すなわち，abcd の面積を s とすると，efgh の面積は s 2 1 になる。この正四角錐と立方体の高さは共通であるので，ともに h と表すことができる。 (立方体の体積)＝(底面積)×(高さ)＝ sh (正四角錐の体積)＝ 3 1 ×(底三角錐の表面積の求め方の公式次は三角錐の表面積を求める公式です。底面が正方形で4つの側面が全て合同な二等辺三角形である正四角錐があ 😩 表面積の方はいたって単純で、三角錐を構成している4つの面の面積を足し合わせれば求めることができます。

Http Math Ymhs Tyc Edu Tw Masterchen Chenyan Teaplan107 Teapncon 107sb6 Ch2 1 E7 94 9f E6 B4 E4 B8 Ad E7 9a 84 E5 9e E7 9b B4 E8 87 E5 E9 Ab 94 E4 B8 8a E8 B2 Pdf

正四角錐表面積求め方

[10000印刷√] おうぎ形面積求め方 194271-おうぎ形面積求め方裏ワザ

数学1 平面図形円とおうぎ形半径と弧の長さ，半径と面積からおうぎ形の中心角を求める。https//math7daifukublogspotjp/ · 扇形の面積の求め方・公式それでは扇形の面積の求め方を考えてみましょう。半円の面積は、もとの円の面積の半分になりますね。同様に、円を6等分してできた扇形の面積は、もとの円の面積の6分の1です。このようにして、面積を求めたい扇形はもとの円と比べてどれくらいの大きさなのか、を考えてみます。上の図のように、扇形の面積は、もとの円の · ハッパ形（レンズ形）のおうぎ形の面積の求め方１　90度のおうぎ形2個－正方形２　（90度のおうぎ形－半径×半径÷２（三角形））×２３　正方形の面積×057 （円周率は314）

円の面積公式

おうぎ形面積求め方裏ワザ

[コンプリート！] 三角形角度問題中学受験 270615-三角形角度問題中学受験

小中学受験図形（1）角度の問題は、等しい角を見つけて書き込む小中学受験図形（2）面積は、三角形かおうぎ形にして求める小中学受験図形（3）となりあった三角形の面積は、比で求める工夫していろいろな角度を求める問題です。平面図形の問題の中でも学習はしやすいところです。角度の問題は、同じようなパターンの問題をまとめて解いてコツをつかんでいくようにしましょう。例1）正三角形や正方形を組み合わせた随時追加していきます。 ★4/22 3ページ追加平行線と角や三角形、平行四辺形など図形の角度を求める問題を集めました。学年中学2年生, 単元平行線と角,三角形,四角形, キーワード平行線と角,角度,三角形,平行四辺形,図形