(中学2年の中点の座標,直線の方程式も使う) 三角形の面積の二等分線 (底辺)×(高さ)÷2 で求められます。 次のように分数の形で書くこともできます。 (面積)= 図1 (1) 2で割ることを忘れる答案が多いので注意しましょう。 次図2の三角形の面積は、 4 × 3=12 ではなく、 4 × 3 ÷ 2=6 に257 = 32 25 7 = 32 (㉜)が、 96−21× 2 = 54(cm) 96 − 21 × 2 = 54 ( c m) です。 54cm 54 c m を 25 7 25 7 に比例配分します。 54× 7 257 = ×1 16 (cm) 54 × 7 25 7 = × 1 16 ( c m) これが、求める小さい球の半径です。 あとは、これを小学生、中学生に分るように、ちょいと丁寧に説明すれば済むだろう。 実際に模型を作るのも間単だ。 さて、ここで、三角形の場合と比べてみよう。 三角形の面積は底(底辺の長さ)×高さを2で割るので、2が出てくる。 ということは、 底
緊急です この円錐の下の円の半径と円錐台の高さの求め方を教えて下さい Yahoo 知恵袋
円錐 高さ 求め方 中学
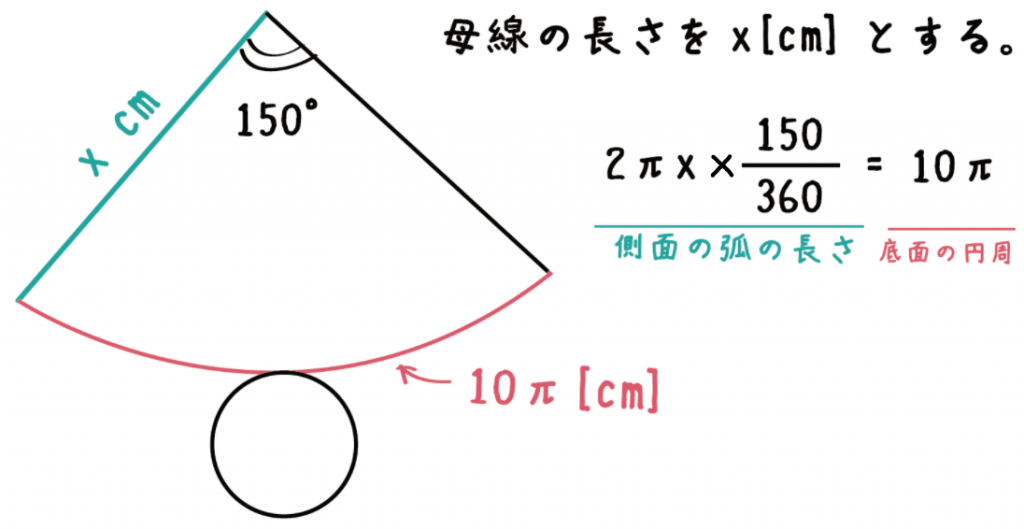
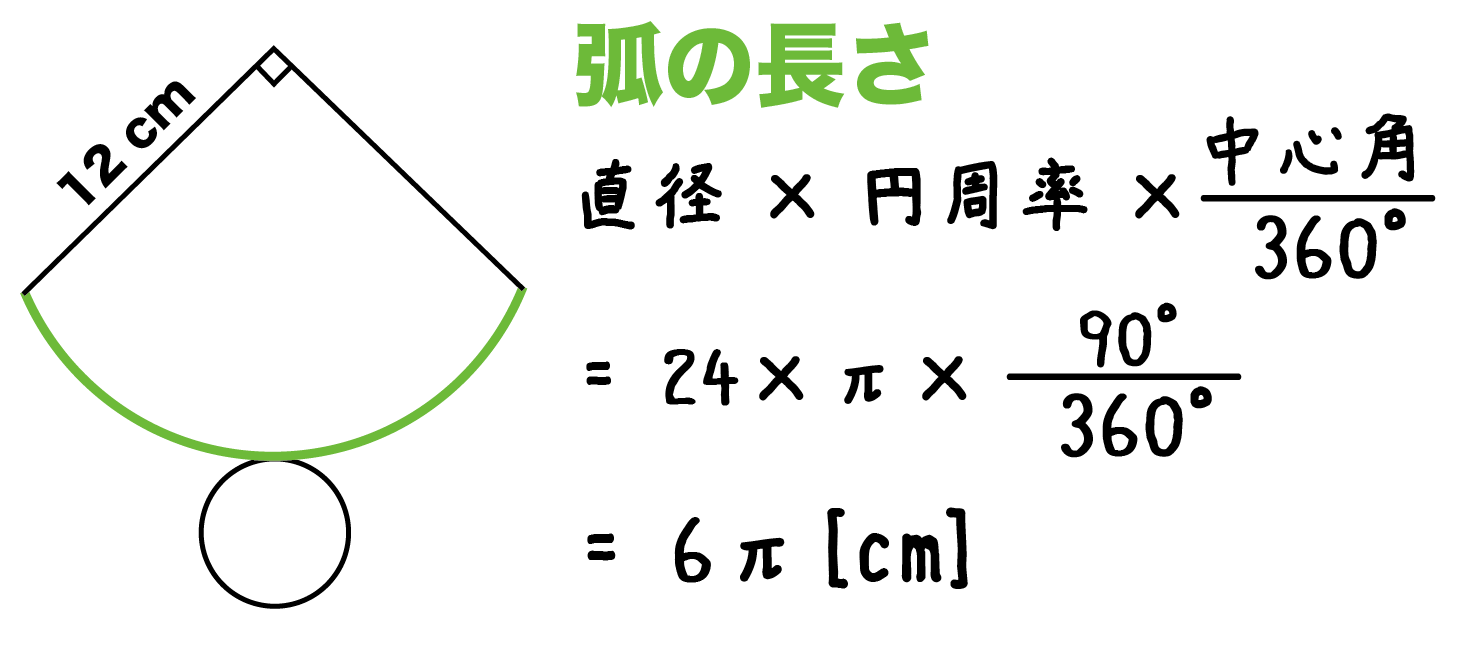
円錐 高さ 求め方 中学- 円錐や角錐の体積の求め方 中学1年数学 Youtube 円錐 体積 公式 求め 方 円錐 体積 公式 求め 方底が楕円として、楕円錐の体積を算出したかった。 keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√(a*b高さは $\textcolor{blue}{4\rm cm}$ 円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。 おうぎ形の弧の長さは、$2×6×π=12π \rm cm$ 大きい円の円周は、$12π×3=36π \rm cm$ 母線の長さは、 大きい円




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
て先に整理した面積の求め方を参照させる。 (例)底面積s6×4 =24 高さh7 自分でノートに見取図をかいて,辺,半径,高さ などに長さを記入する。 見取図の書き方ができるかどうか確認する。 ま と め 今日の学習のまと めをする。 錐体の体積= めっちゃ簡単! ? 円錐の体積の求め方を解説 投稿日:年6月25日 こんにちはこんばんは! taraといいます。 6月も終わりを迎えようとしている今日この頃ですが、 空模様はまだまだ梅雨真っただ中ですね。 僕自身ジメジメした気候は嫌いなんで、中学 数学空間 空間図形 角柱・角錐(すい)・円柱・円錐の体積の求め方 角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ここで紹介している内容
円すいの体積の公式 底円の半径を r 、高さを h とすると 上図の円錐の体積は 体 積 底 面 積 高 さ 体積 V = 底面積 × 高さ × 1 3 = r × r × 314 × h × 1 3答えを求めておくと 高さは $$6^2=2^2x^2$$ $$x=4\sqrt{2}$$ 体積は $$4\pi \times 4\sqrt{2} \times \frac{1}{3}$$ $$=\frac{16}{3}\sqrt{2}\pi cm^3$$ となります。 これで 展開図で出されても大丈夫ですね! 半径がわからないパターン ここまでずっと 円錐の高さのことばかり言ってきましたがS:へー。あれ、さっきの半球の体積は、底面が円で高さrの円錐の2倍ですよ。 円錐×2=半球 円錐×3=円柱 ということですか。 t:つまり、cがaに対して何倍になっているのかで、1/2か、1/3か、2/3かが決まるということです。
円錐の底面積と高さを掛け合わせましたら、後はその値を3で割ってください。 したがって、円錐の体積を求める式はこのようになります。 それでは、実際に円錐の体積を求める式に数字を入れて計算してみましょう。 次のように円錐の底面の半径と高さが与えられた時の体積を求めてスマートフォン 円錐台の底面と上面の半径と高さから体積、側面積、表面積を計算します。 底面半径 r1 上面半径 r2 高さ h 体積 V 側面積 F 表面積 S お客様の声 アンケート投稿 よくある質問 リンク方法 円錐台の体積 110 /138件 表示件数 1 1632 歳未満 中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを 中学数学 円錐の高さの求め方 頻出パターン なぜか分かる 三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ 円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生 高さの分からない円すい展開図 どう




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



緊急です この円錐の下の円の半径と円錐台の高さの求め方を教えて下さい Yahoo 知恵袋
(底面積)×(高さ)×1/3 この 1/3 を忘れてしまってはダメだよ。 《円錐の高さの求め方》 円錐の体積=底面積×円錐の高さ÷3であることから 円錐の高さ=円錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=10×10×314=314 よって求める円錐の高さ=1570÷314×3=15(cm) 答え 15cm 問題④円錐の表面積の求め方 公式と計算例 中学数学円錐の中心角の求め方3パターン なぜか 円錐の表面積や体積の求め方!すぐ分かる方法を慶応生が解説 円錐を カット する!体積は どうなる? 名寄・算数数学教室より 数学円錐の高さの求め方



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
この記事の目的:錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する. はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると? 最後に円錐となる回転体の側面積・表面積の求め方中学1年数学:空間図形 😋 その後、底面積を出すことで、円錐の表面積を計算できます。 「なんだそれ・・・?」 そう思ったそこのあなた! 安心してくださ 結論からいうと、円すいを開いた時にできるおうぎ形の中心角は、母線と底面の半径の関係で決まってしまいます。 そのため、母線の長さをR、底面の半径をrとした場合、以下の公式が成り立ちます。 例題に当てはめてみると、このようになります。 \begin {eqnarray} 360°×\frac {3} {12} = 360°×\frac {1} {4} = 90° \end {eqnarray} この公式を使えば、かなりのスピードで



円錐の高さの求め方 至急求む 写真の図は 底面の円の半 Yahoo 知恵袋




円錐の体積の求め方 公式 小学生 中学生の勉強
(円錐の高さ) = √(斜辺の二乗) (その他の1辺の二乗) = √ (12)² – 3² = √135 になるね。 おめでとう^_^ 円錐の高さもゲットだね! まとめ:円錐の高さの求め方は三平方の定理でとどめ! 円錐の高さを求めるのはむずそう。錐の体積 = 底面積 × 高さ× 1 3 赤い円 の円周の長さは 直 径 直 径 × 314 = 3 × 2 × 314 = 14 c m




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




中3 三角形の相似 円錐の体積比 日本語版 Youtube
中学数学空間図形 円すいの表面積の求め方 空間図形 円すいの表面積の求め方 円すいの表面積の求め方の手順とポイントがよくわかりません。 進研ゼミからの回答 次の3つが大きなポイントです。 ・底面(円)と側面(おうぎ形)に分けて求める ・円の円周とおうぎ形の弧の長さ動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru問題7 (球と円錐の体積) 右の図のような半径9cmの半球があります。この半球と等しい体積の円 すい 錐について考えます。円錐の底面の半径が9cmであるとき,円錐の高さは何cmか求めなさい。



円錐とは 体積 表面積の公式や求め方 受験辞典



1
円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!考え方は同じです。微小区間の体積 dV を求めます。 高さは dx,底面の半径は なので, となり こんな感じになるね! 扇形と円で比例式を立てて、 4π 12π = x 360 4 π 12 π = x 360 ∴ 12π× x = 4π× 360 12 π × x = 4 π × 360 ∴ x = 4π 12π × 360 x = 4 π 12 π × 360 ∴ x = 1 x = 1 だから、1°だね! はかせちゃん 扇をくるくるくるくるくるくる今回は、一次関数によって表された図形の面積の求め方について解説していきたいと思います! 苦手に感じている人も多くいる問題だと思いますが、高校入試の問題に繋がってくる可能性が高いので、必ずマスターして抑えておくようにしましょう! では、今回も頑張っていきましょう! あす




体積の求め方 計算公式一覧




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ
次に高さは、立方体の半分の高さとなっているので、 a×1/2 です。 したがって、底面積と高さを使って公式をつくるためには、 a 2 ×a×1/2×x=a 3 ×1/6 とならなくてはいけません。 このxについての方程式を解くと、 x=1/3 が出てきます。 円錐の表面積 体積計算の簡単な求め方を解説 公式を証明しよう 中学数学で習う円錐の表面積体積の求め方 円柱とはどう違うんだっけ 表面積って何か公式あったよね なんて忘れかけていませんか 高校数学大学受験でも頻出の円錐 今一度円錐の求め方公式の覚え方を再確認しましょう問題 下の図のように、底面の半径が \(28cm\),母線の長さが \(100cm\) の円錐に 球が内接しています。この球の半径を求めなさい。 解説 平面における、「三角形と内接円の関係」とほぼ同じです。 空間



中学数学 円すいの表面に糸を巻く 中学数学の無料オンライン学習サイトchu Su




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
Keisanより 長径a,短径bの楕円の面積S=πab、半径rの円の面積はS=πr 2 ですので、直円錐の体積の半径rに開平√ (a*b)を計算して代入すれば、楕円錐の体積が求まります。 5 2338 男 / 歳未満 / 学生 / 役に立った / 使用目的 これからの数学との戦い ごさて、円錐の表面積や中心角の求め方はご理解いただけましたか? 計算量が多いし、ちょっとややこしいですよね そんなあなたに活用してほしいのが 円錐の側面積と中心角を一瞬で求めてしまう裏ワザ公式です! まぁ、受験ではほとんどの人がこの裏ワザ公式を利用することになると思い



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の公式 数学fun




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




高さの分からない円すい展開図 どうやって立体の体積を求めるの




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント




公式を図解 すい体の体積 円すいの表面積の求め方




公式を図解 すい体の体積 円すいの表面積の求め方



円すいの高さの求め方を教えて下さい できたらr でお願いします ど Yahoo 知恵袋




高さの分からない円すい展開図 どうやって立体の体積を求めるの




21番は高さの求め方 22番は母線の求め方を教えてほしいです Clear




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




解き方を分かりやすく教えて下さい 答えは2倍です Clear




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



1




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



数学 円錐の高さの求め方分かりますか 高さが分からないと体積も求め Yahoo 知恵袋




角錐 円錐の体積と表面積の公式 数学fun



円錐とは 体積 表面積の公式や求め方 受験辞典




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
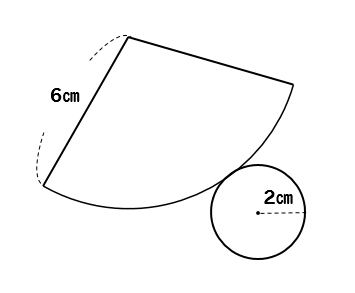



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積の求め方 公式と計算例




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




角錐 円錐の体積と表面積の公式 数学fun



円すいの高さの求め方を教えて下さい できたらr でお願いします ど Yahoo 知恵袋




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




角錐 円錐の体積と表面積の公式 数学fun



円錐とは 体積 表面積の公式や求め方 受験辞典



円錐とは 体積 表面積の公式や求め方 受験辞典




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




なぜ 切り取られた部分の円錐の高さが2になるのかがわかりません Clear




角錐 円錐の体積と表面積の公式 数学fun




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




高さの分からない円すい展開図 どうやって立体の体積を求めるの
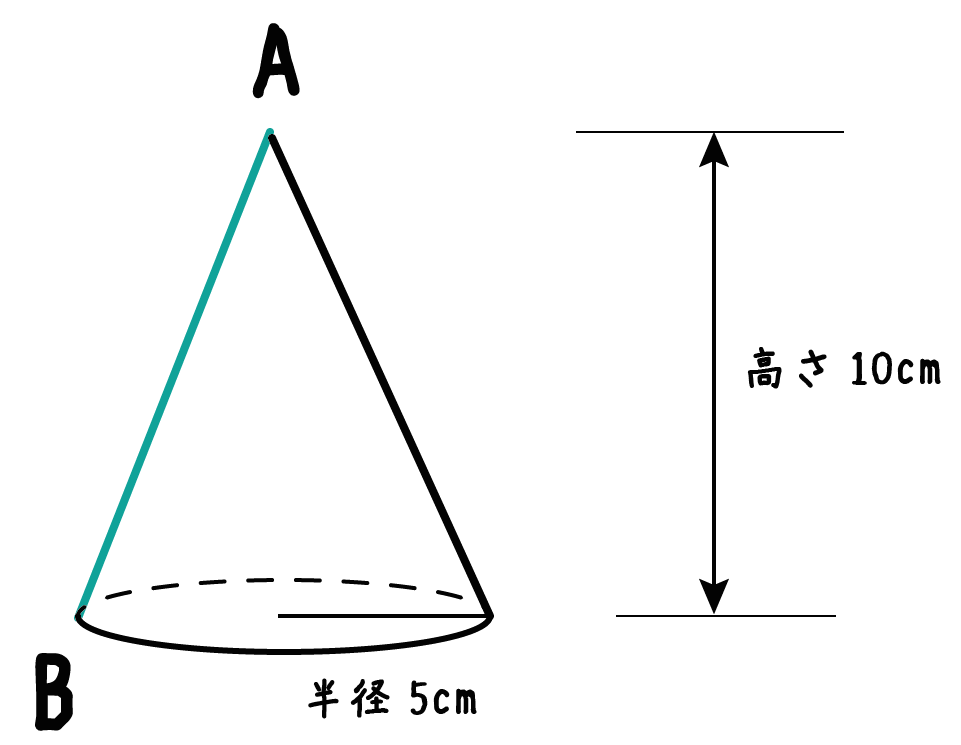



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例
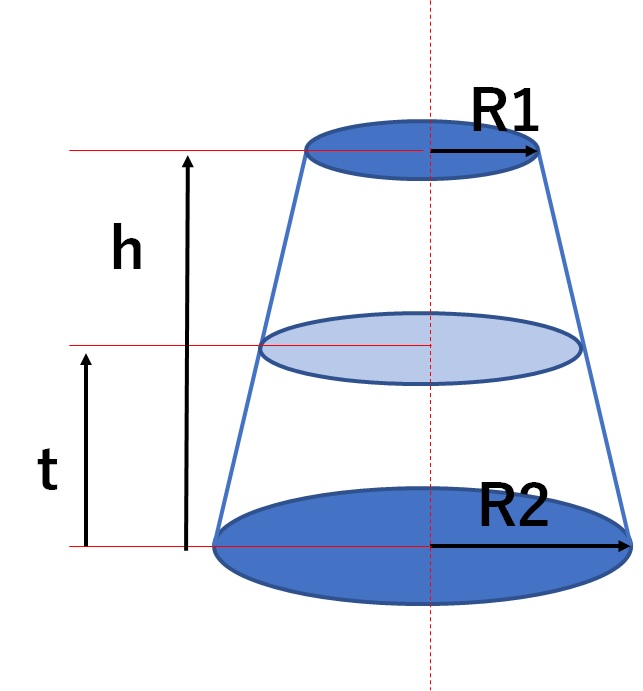



円錐台の体積を半分にする高さを計算 高精度計算サイト




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




高さの分からない円すい展開図 どうやって立体の体積を求めるの




高校入試対策数学 円錐に関する対策問題 Pikuu




公式を図解 すい体の体積 円すいの表面積の求め方




高さの分からない円すい展開図 どうやって立体の体積を求めるの



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
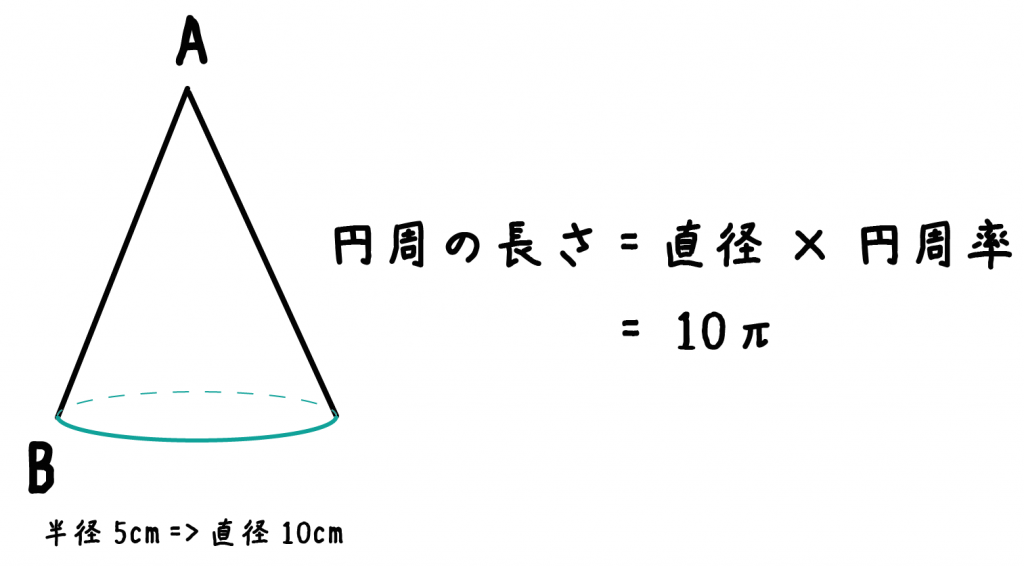



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



角錐と円錐の体積の求め方は 同じなんですか 円錐が底面 高さ Yahoo 知恵袋




半径5分の12cm 高さ6cmの双円錐の体積を求めるのに Clear




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 円錐の中心角の求め方 3パターン なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
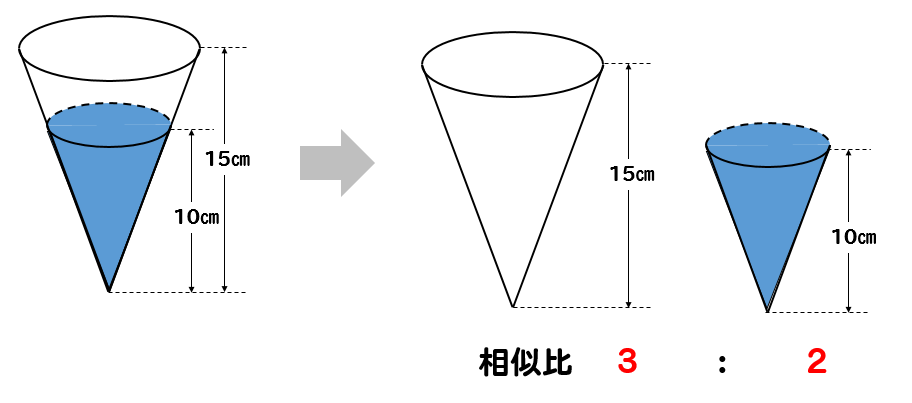



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




中3数学 円錐の高さと体積 5分で学習 Youtube




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
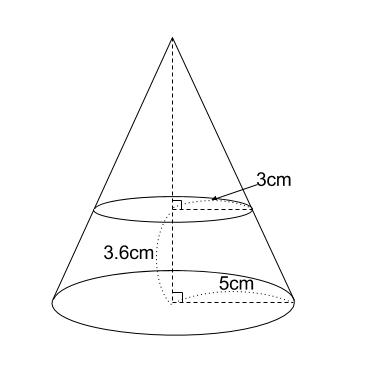



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
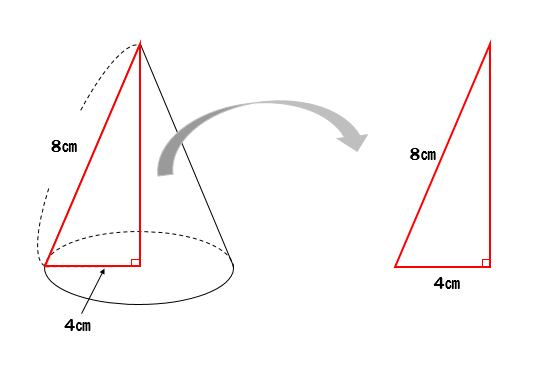



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




空間図形14 円すい台の体積 Youtube




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円錐とは 体積 表面積の公式や求め方 受験辞典




円錐の体積の求め方 公式と計算例




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
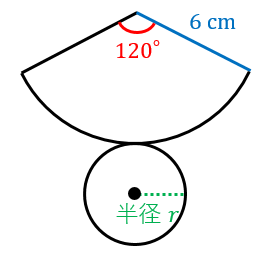



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




高さの分からない円すい展開図 どうやって立体の体積を求めるの




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




公式を図解 すい体の体積 円すいの表面積の求め方
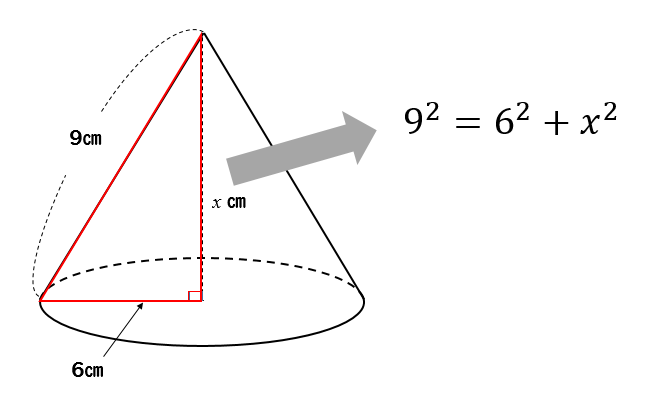



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




円錐の体積を求める Youtube




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
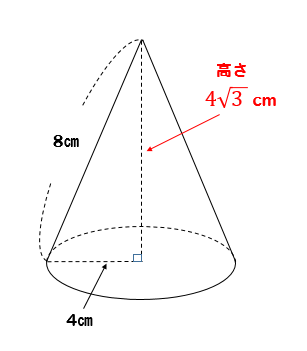



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




円錐の体積ってなんであの公式なの Webty Staff Blog




体積の求め方 計算公式一覧
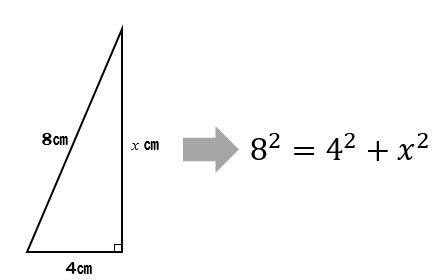



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ
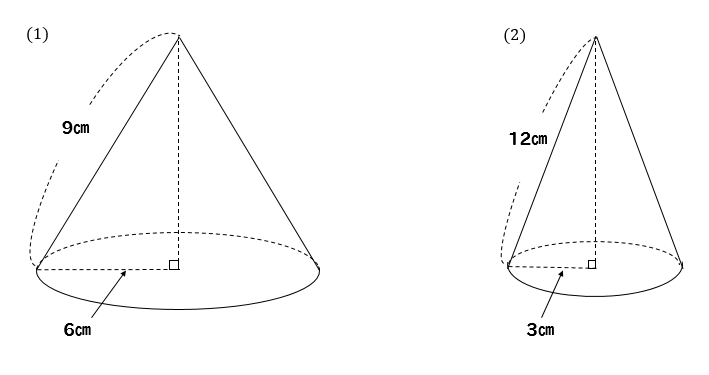



三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ



中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
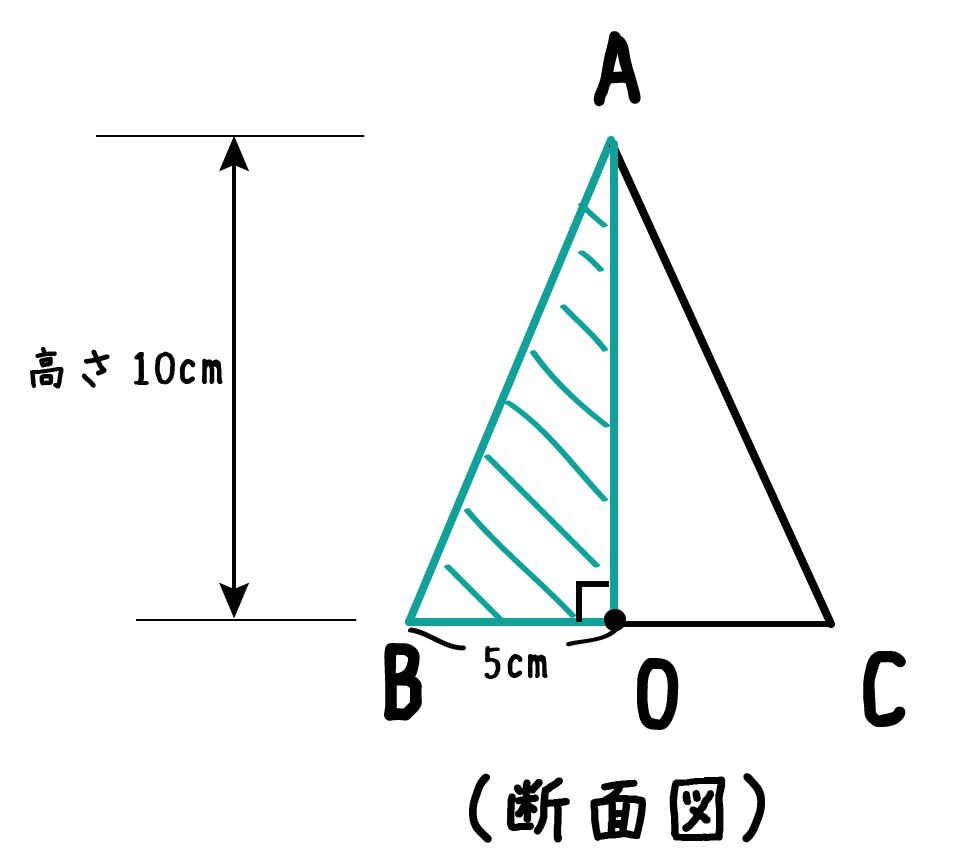



中学数学 円錐の 母線の長さ がわかる2つの求め方 Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿