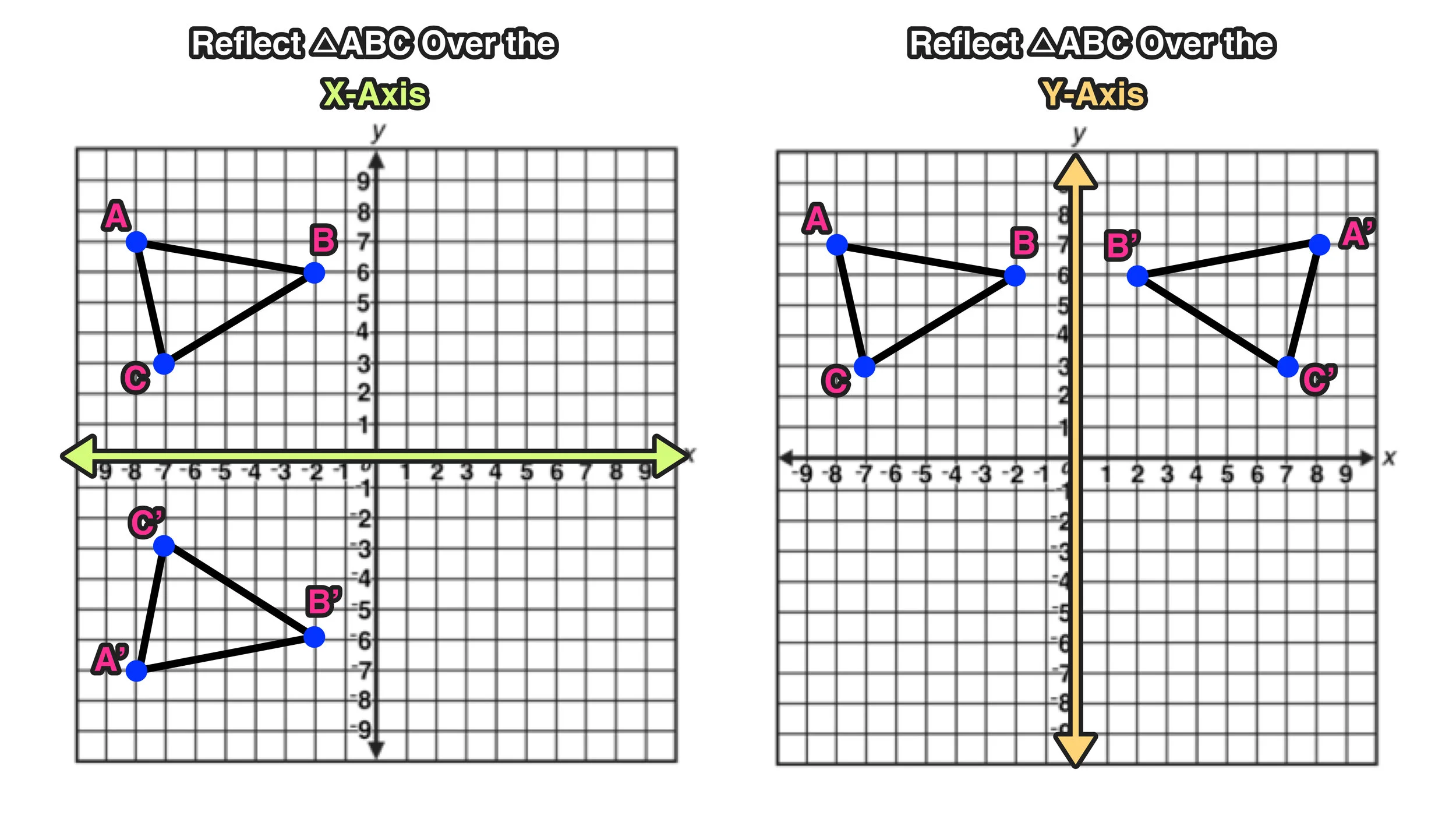
180˚ rotation about the origin (clockwise or counterclockwise would give you the same result)Reflection in the line y = x Try to work out the coordinates of the reflected points before you reveal the answer 1) If the point (2, 3) is reflected over the xaxis what is the new point?X and y for reflection over the xaxis Unit 2, 93 Write the coordinate notation rule in terms of x and y for reflection over the xaxis ( , )→( ,− ) Line of reflection y = 0 Unit 2, 93 a After a reflection across the xaxis, which direction will the arrow

Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
Reflection across the line y x calculator
Reflection across the line y x calculator-Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlphaTo play this quiz, please finish editing it Q Reflect the point (2, 4) over the yaxis Q Reflect (6, 3) over the line xaxis Q You want to reflect a figure over the horizontal line shown What directions would you give?



How To Find A Reflection Image
Active 1 year, 10 months ago Viewed 1k times 0 We have that The linear transformation matrix for a reflection across the line y = m x is 1 1 m 2 ( 1 − m 2 2 m 2 m m 2 − 1) So reflection across the xaxis would be 1 1 ( 0) 2 (Translation Function Formula f (x, y) = 0 → f (x a, y b) = 0 Unlike the translation of a point, change the signs of a and bJust approach it stepbystep For each corner of the shape 1 Measure When the mirror line is the yaxis we change each (x,y) into (−x,y) Fold the Paper
Doesn't f(x) reflect over the xaxis So lets say I had f(x) = x^2 (using x^2, because its easier to see on my calculator where it reflects) If I put f(x) = x^2 that would just reflect it over y=0 so the origin And adding two to x^2 2 would just raise itWhy does the output of my astable multivibrator using an opamp turn into a triangular wave?The linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (m
Reflections A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflectionA reflection is a type of rigid transformation, which means it changes the position or orientation of an image without changing its size or shape A reflection does this by flipping an image across a fixed line just like a mirror!Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =




Reflect Over X Axis Calculator Calculator Academy




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
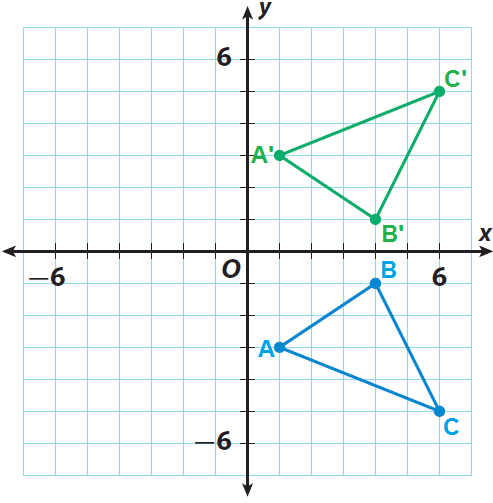
The image of the point with coordinates (1,1) under the reflection across the line y=mxb is the point with coordinates (9,5) Find mb Thanks!Reflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC hasThe resulting orientation of the two figures are opposite Corresponding parts of the figures are the same distance from the line of reflection Ordered pair rules reflect over the xaxis (x, y), yaxis (x, y), line y = x (y, x) The following diagram shows how to reflect




Reflection Rules How To W 25 Step By Step Examples




Learn About Reflection Over The Line Y X Caddell Prep Online
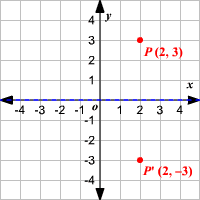
This calculator helps you to find the point reflection A, for the given coordinates of A (x,y) Just select an axis from the dropdown and enter the coordinates, the point reflection calculator will show the result Just copy and paste the below code toCommon Core Math Geometric Reflection over Y= 2Reflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $




Hwq 1 12 15 Evaluate The Definite Integral No Calculator Please Ppt Video Online Download



Reflections
To perform a geometry reflection, a line of reflection is needed;A free graphing calculator graph function, examine intersection points, find maximum and minimum and much more This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy0 Linear transformation reflected across yaxis?
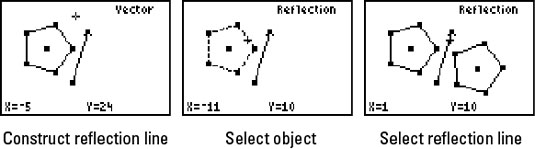



Reflect Geometric Objects With The Ti 84 Plus Dummies




Calculating Grease Quantity Frequency
To perform a geometry reflection, a line of reflection is needed;Play this game to review Geometry B(2, 4) Reflect over the line y = x Preview this quiz on Quizizz B(2, 4)Reflect over the line y = x Reflections over y = x and y = x DRAFT 8th grade 274 times Mathematics 54% average accuracy 10 months ago jnugeness 0 Save Edit Edit Reflections over y = x and y = x DRAFT 10 months ago by Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change size




2x2 Matrix Addition And Subtraction Calculator




Inverse Trig Functions
Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History reflection across the line y=x 0 43 1Q) and (r, s) (In the graph below, the equation of the line of reflection is y = 2/3x 4 Note that both segments have slopes = 3/2, and the shorter segments on both sides of the line of reflection also have slopes = 3/2 If you are using a xy coordinate axes drawn with a 11 aspect ratio, you can find preimage and image points by just countingA reflection is a flip over a line You can try reflecting some shapes about different mirror lines here How Do I Do It Myself?



Geometry Objectives 6 8 Part 1 Ppt Download



What Does It Mean To Reflect Over The Y X Line Quora
Answer (1 of 4) You really need to draw this out to get a real feel for the answer and what is happening Think of y=2 as a horizontal mirror line Cutting through the yaxis at 2 The point (3,1) will reflect from below the xaxis over the mirror line and end up, above it, keeping the xcoorB Reflection of a figure across a line 6 Click on the button "0, 1 or 2 reflections" in order to have 1 reflection To generate a figure such as a triangle, rectangle or an even more complicated figures, click anywhere on the plot screen to plot connected points and adjust the position of these points by dragging them90˚ counterclockwise rotation about the origin OR 270˚ clockwise rotation about the origin Which rigid motion maps A(3, 1) to A'(3, 1)?




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Rules How To W 25 Step By Step Examples
The fixed line is called the line of reflection, and in the image below, it's where the ground meets the waterNotice that the points from the actual buildingReflection across the line y = x in 3 Dimensions?A reflection in a line produces a mirror image in which corresponding points on the original shape are always the same distance from the mirror line The reflected image has the same size as the original figure, but with a reverse orientation




Erlang C Calculator Excel Including Shrinkage




Axis Of Symmetry Calculator With Steps Formula Equation
Free functions symmetry calculator find whether the function is symmetric about xaxis, yaxis or origin stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyA translation of 2 units down followed by a 180° rotation about the point (1, 2) B a reflection over the line x = 0 followed by a reflection over the line y = 4 C a reflection over the line x = 1 followed by a translation of 2 units down D a translation of 12 units right and 2 units down E a rotation of 180° about the point (1, 4) F a👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Rotation Rules
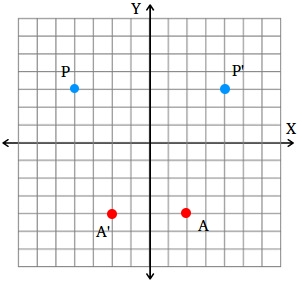
A shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinateReflection over the line y = x Which rigid motion maps A(3, 1) to A'(1, 3)?For reflection about a vertical axis (x = 1), we need only be concerned with the xcomponents of the vertices Given any point (x, y), the new x' value would be the distance 'd' from the reflection axis (x (1)), then inverted for reflection abo




How To Find A Reflection Image
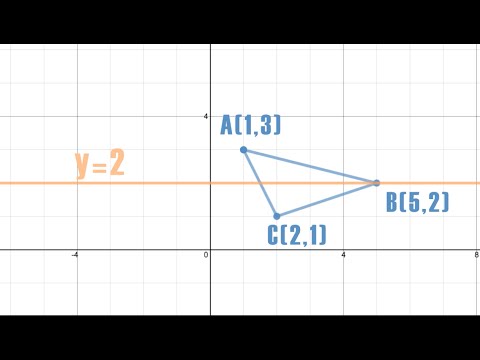



Reflection Across Y 2 Silent Solution Youtube
The resulting orientation of the two figures are opposite Corresponding parts of the figures are the same distance from the line of reflection Ordered pair rules reflect over the xaxis (x, y), yaxis (x, y), line y = x (y, x)3 people liked this ShowMe Flag ShowMe Viewed after searching for reflection over the line y=x reflection over yaxis Reflection over y=x is over of equals percent over 100 reflect over x= 1 You must be logged into ShowMeReflection, Geometric Transformations Click and drag the blue dot to see it's reflection across the line y=x (the green dot) Pay attention to the coordinates




Reflection Rules How To W 25 Step By Step Examples




The Best Graphing Calculators Of
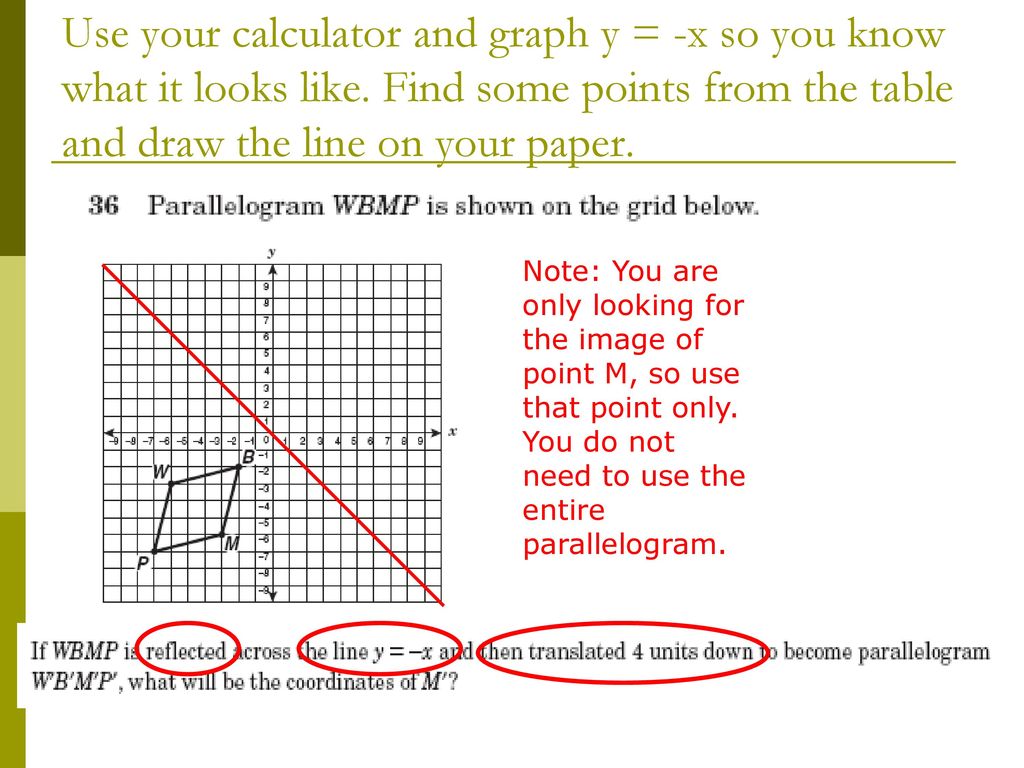
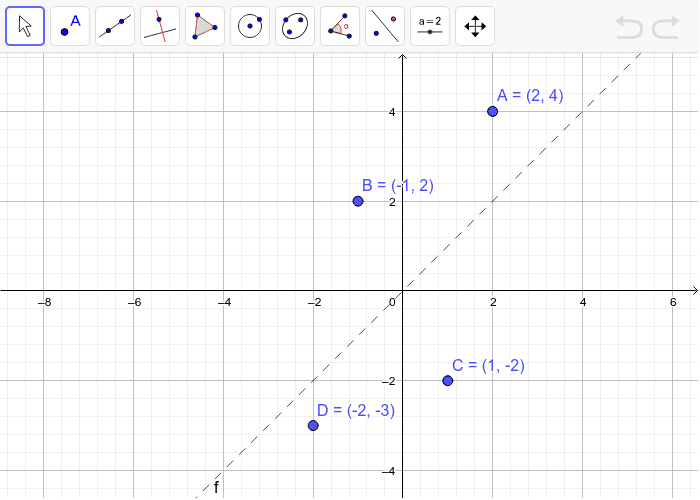
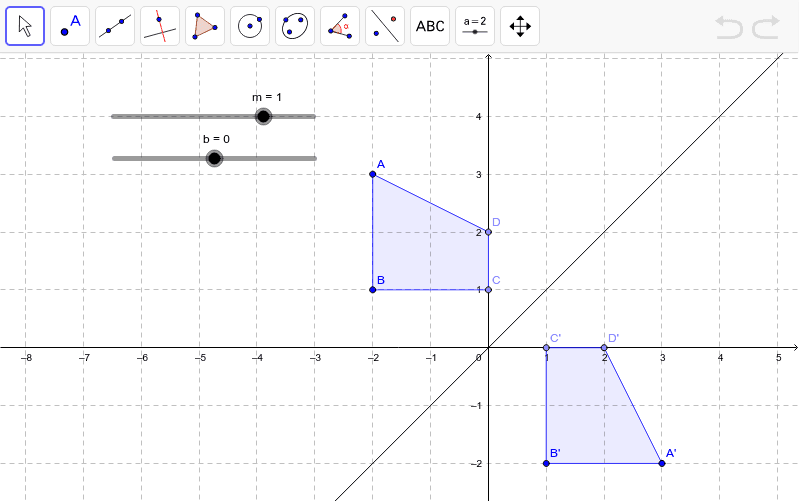
Hot Network Questions Distribution of argmax of betadistributed random variables Why is the Arctic melting, but the Antarctic doing great?Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the form y = m x b y = m x b m = − 1 m = 1 b = 0 b = 0And also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxis




How To Find A Reflection Image



What Is The Reflection Of The Point 1 2 In The Line Y 3 Quora
Points reflected across x axis Loading Points reflected across x axis Points reflected across x axis Log InorSign Up − 7, − 6 1 − Calculus Tangent Line example Calculus Taylor Expansion of sin(x) example Calculus Integrals example Calculus Integral with adjustable bounds Reflect Over XAxis Definition Reflection over the xaxis is the process of producing a coordinate point that is mirrored across the xaxis of the coordinate plane That is it has the same X coordinate and opposite y4 coordinate For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflection




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Stramtoarea Cartier Empiric Find Y Function Calculator Tripalamode2nous Com
2) If the point (4, 6) is reflected over the yaxis what is the new point?For a reflection in the line y=x $$\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$$ Example We want to create a reflection of the vector in the xaxis $$\overrightarrow{A}=\begin{bmatrix} 1 & 3\\ 2 & 2 \end{bmatrix}$$ In order to create our reflection we must multiply itA 180° clockwise rotation about the origin and then a reflection across the xaxis A reflection across the xaxis and then a translation by the rule (x, y) (x10, y 9) A translation by the rule (x,y) (xy9) and then a 180° clockwise rotation about the origin A 90° clockwise rotation about the origin and then a reflection across the




Solved The Function F Defined By F X X2 Is Graphed In The Chegg Com




Basic Understandings Pdf Free Download
Q ∆QRS contains the points Q (4, 2) R (5, 1) S (3,7) If the triangle is reflected across the yaxis, what will S(Turn on #3 and #4 below to begin exploring When a figure is reflected over the line y=x, notice that the coordinates change order We can also reflect a figure in the coordinate plane in any point on the coordinate plane Here's a dart reflected in the point (12,10) The point the dart is reflected over is called, you guessed it, the point of reflection



1 9 Introduction To Parent Functions Holt Algebra




1 8 1 9
In this video, you will learn how to do a reflection over the line y = x The line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 For triangle ABC with coordinate points A (3,3), B (2,1), and C (6,2), apply aSolution for L6 Reflections find the coordinates SVY Write the coordinates of the vertices after a reflection across the yaxis E 101v F X 10 G 10 10 D(5,Reflection around y=x Loading Reflection around y=x Reflection around y=x Log InorSign Up Here is an example of another kind of reflection that will frequently arise in our discussion of functions What happens when we replace our xvalue with our yvalue and our yvalue with our xvalue?



1



2




Transformation Reflection Over The Line Y X Youtube




Linear Algebra Reflection In Any Linear Line Y Ax B Youtube




Which Point Would Map Onto Itself After A Reflection Across The Line Y X 4 4 4 0 0 4 4 4
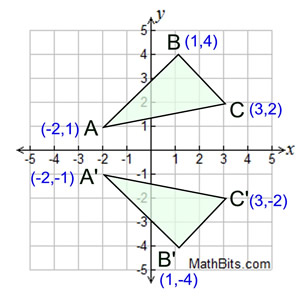



Reflection Mathbitsnotebook Geo Ccss Math




Reflection Transformation Matrix




Precalculus Notes Chapter 1
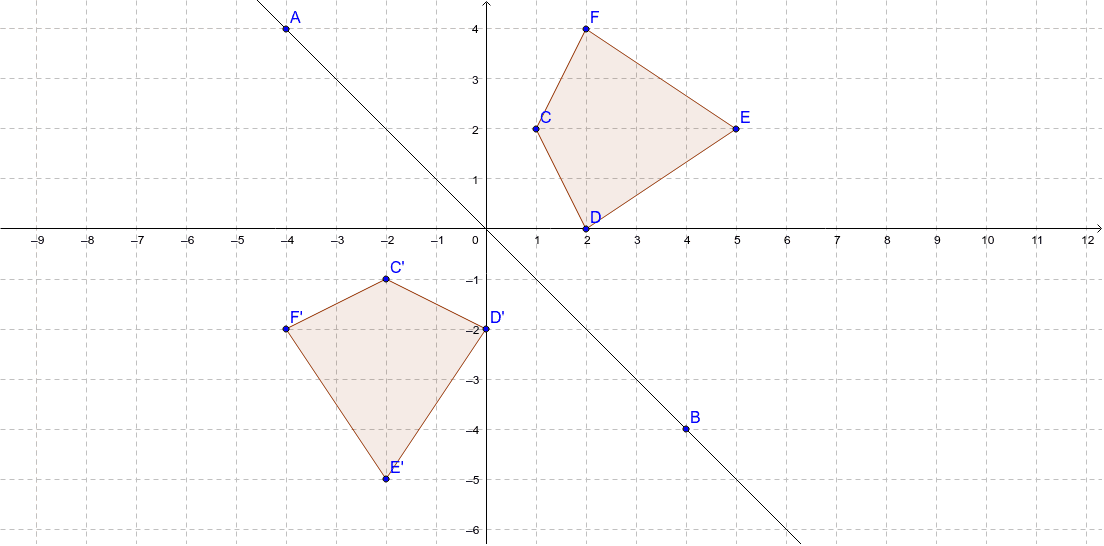



Reflection Over Y X Geogebra
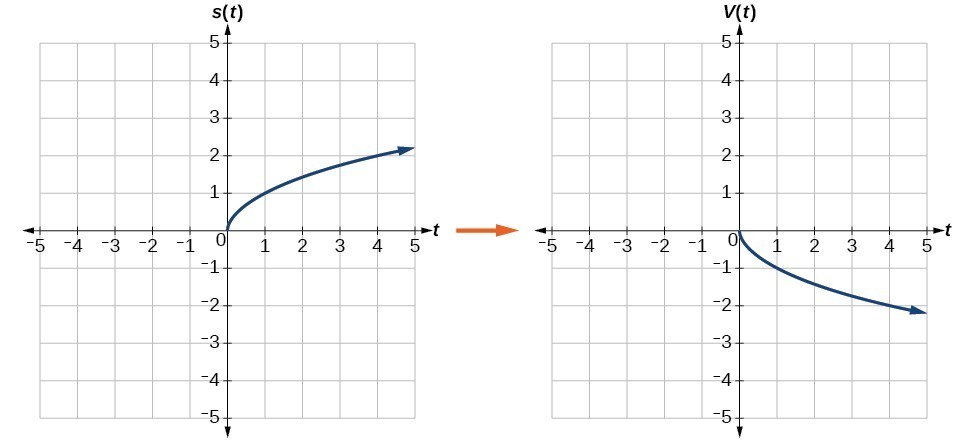



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
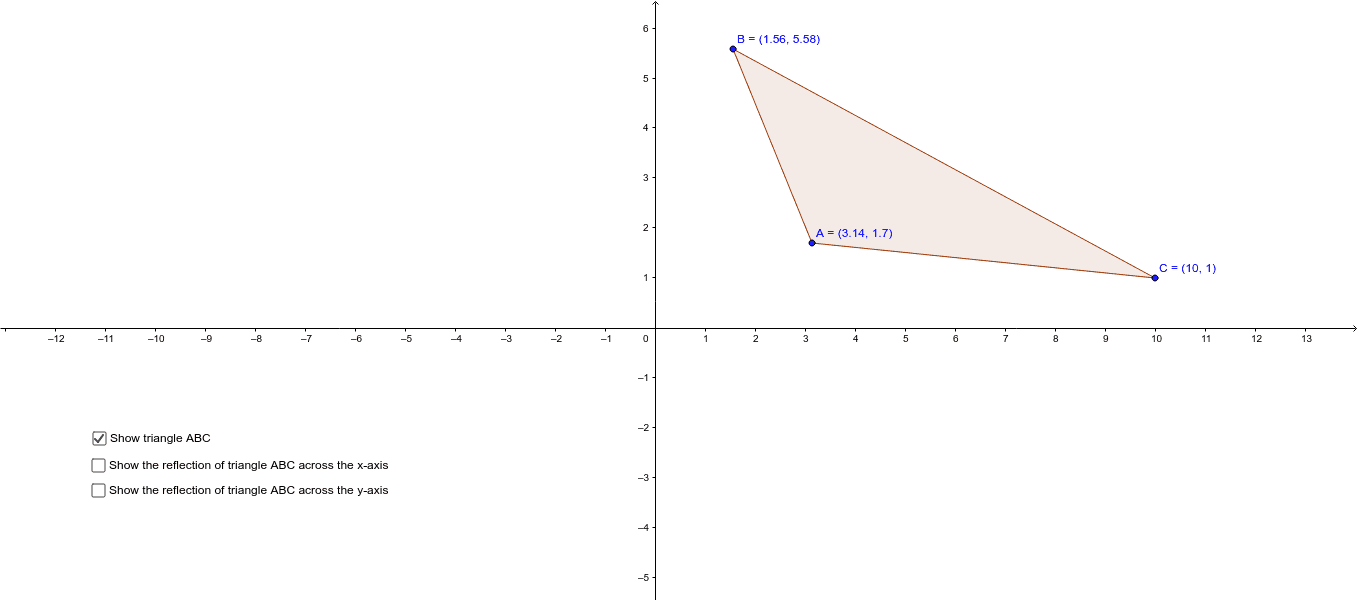



Reflecting A Triangle Across The X Axis And The Y Axis Geogebra
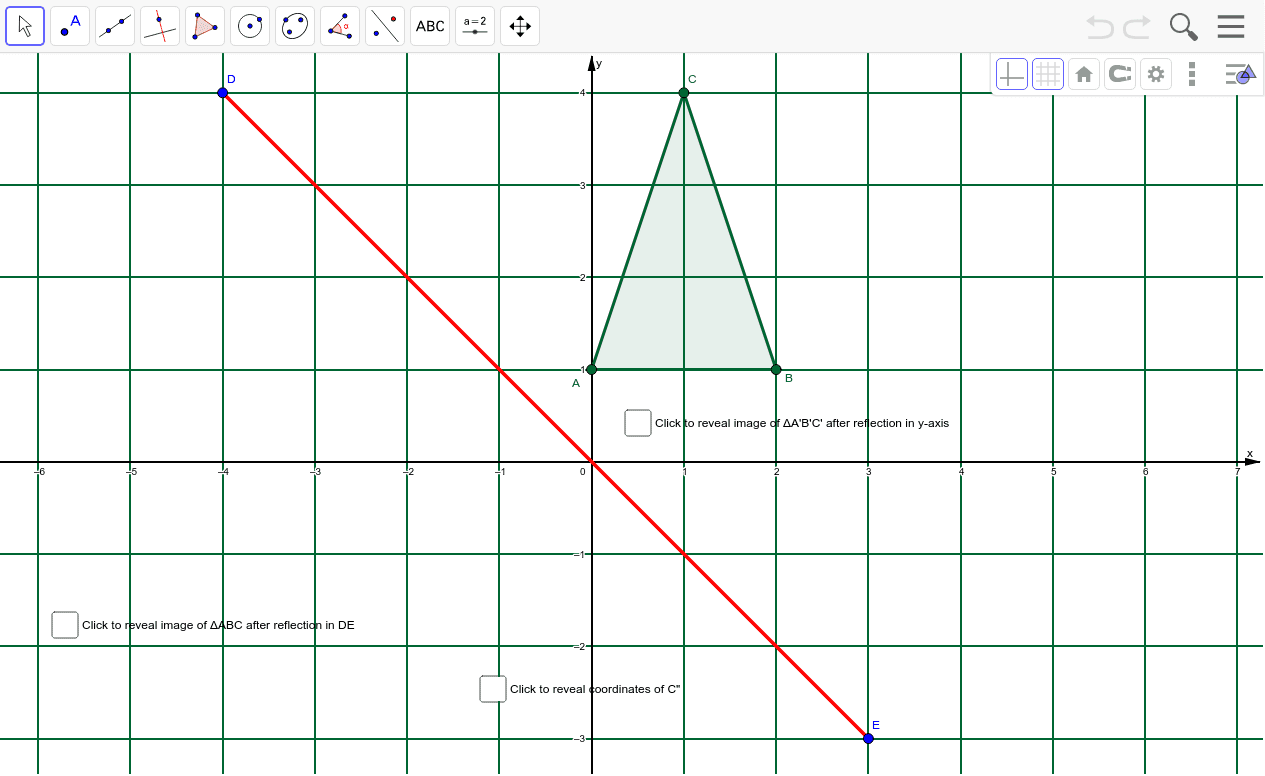



Reflection In The Line De Followed By Y Axis Geogebra



Inverse Functions
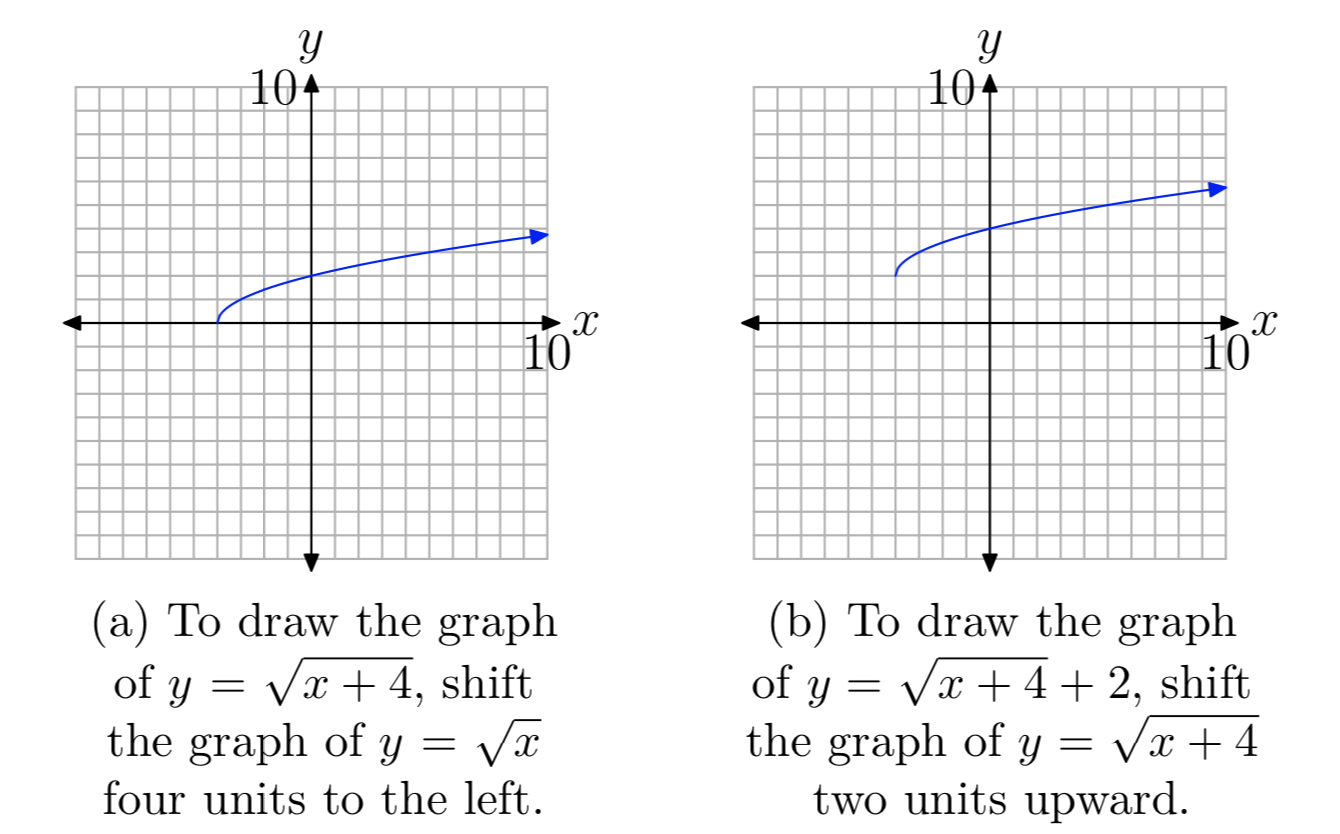



9 1 The Square Root Function Mathematics Libretexts
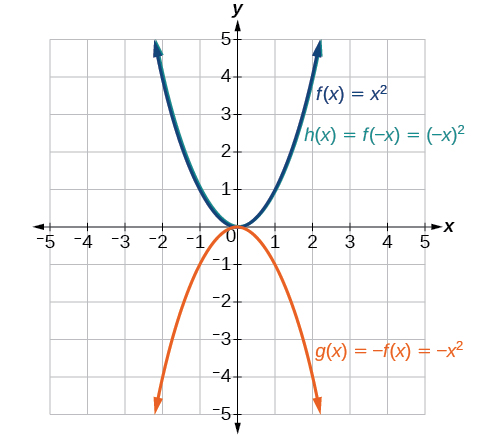



Transformations Of Functions College Algebra
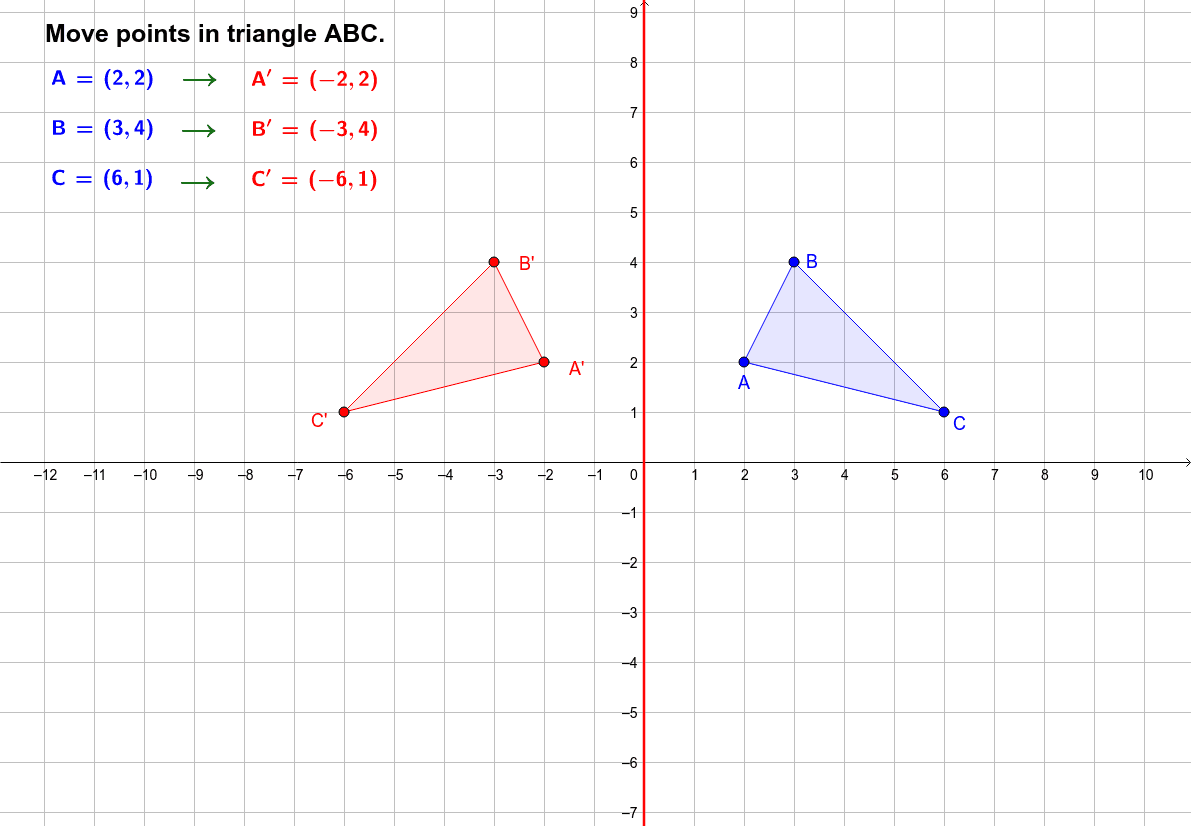



Reflection Over Y Axis Demonstration For Math 8 Geogebra




Vswr Return Loss Calculator Electrical Engineering Electronics Tools




Scaling Reflecting Parabolas Video Khan Academy



Transformation Reflection Over X Axis




Best Calculator For Chemistry Top Scientific Calculator Of 21
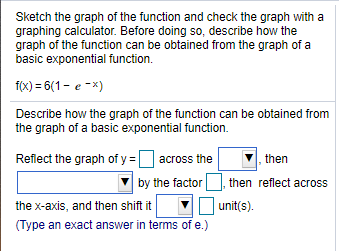



Solved Sketch The Graph Of The Function And Check The Graph Chegg Com



Reflection Over The Y Axis Geogebra



Reflect Over X Axis Calculator Calculator Academy




3x3 Matrix Multiplication Calculator




How To Find A Reflection Image




Solved Sketch The Graph Of The Function And Check The Graph Chegg Com



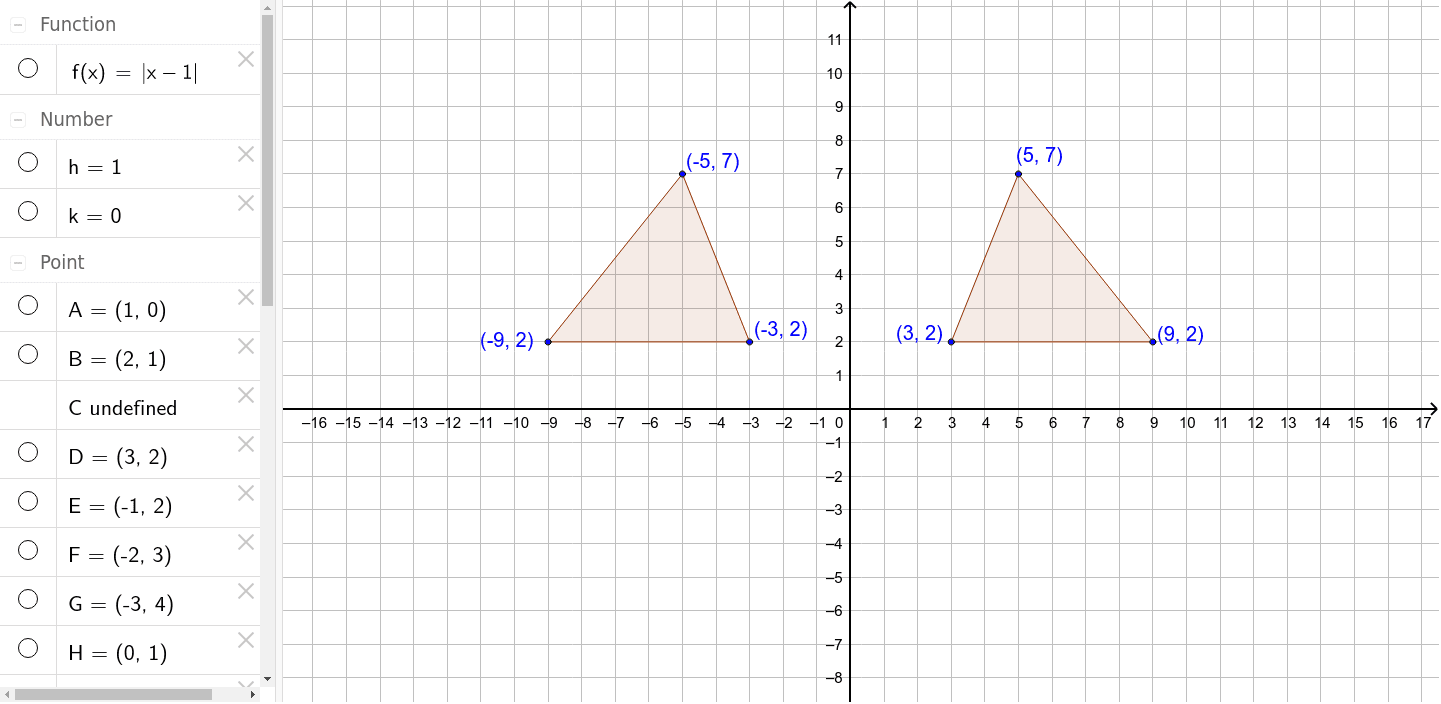
View Question Reflection Across The Line Y X
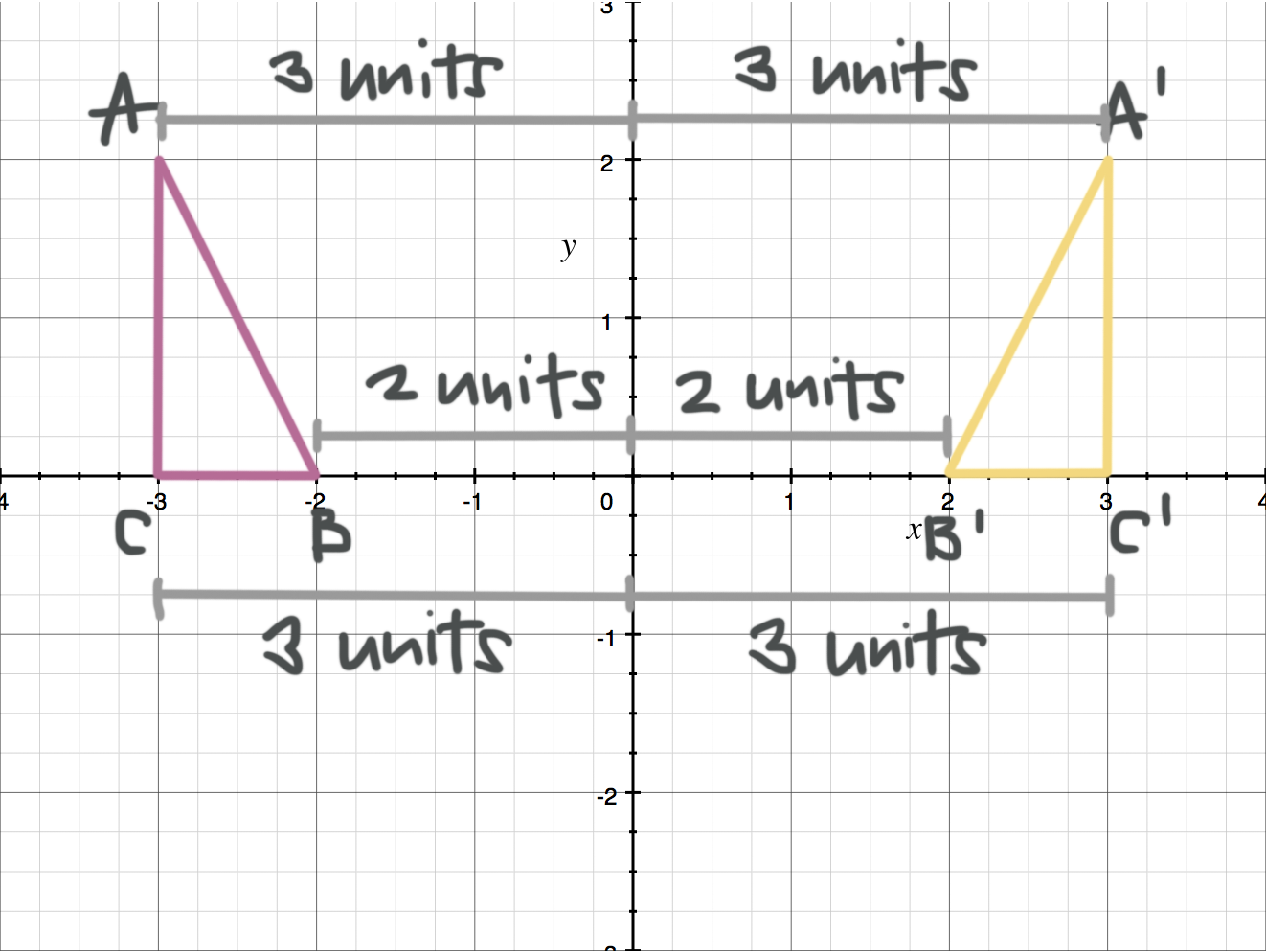



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflections Across Y X Geogebra



Reflection Across Y 2



Desmos Accessibility



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflection Transformation Matrix




Solved Sketch The Graph Of The Function And Check The Graph Chegg Com
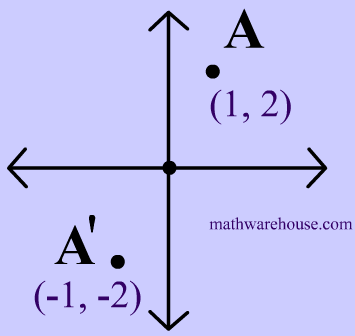



Point Reflections Formula And Examples Explained With Applet Examples And Practice Problems Center At Origin And At Any Arbitrary Point




Calculator Wikipedia




Reflection Transformation Matrix




Solved 21 T Math Geo T1 Cbt Section 1 No Calculator Section Question 1 4 Based On The Brainly Com



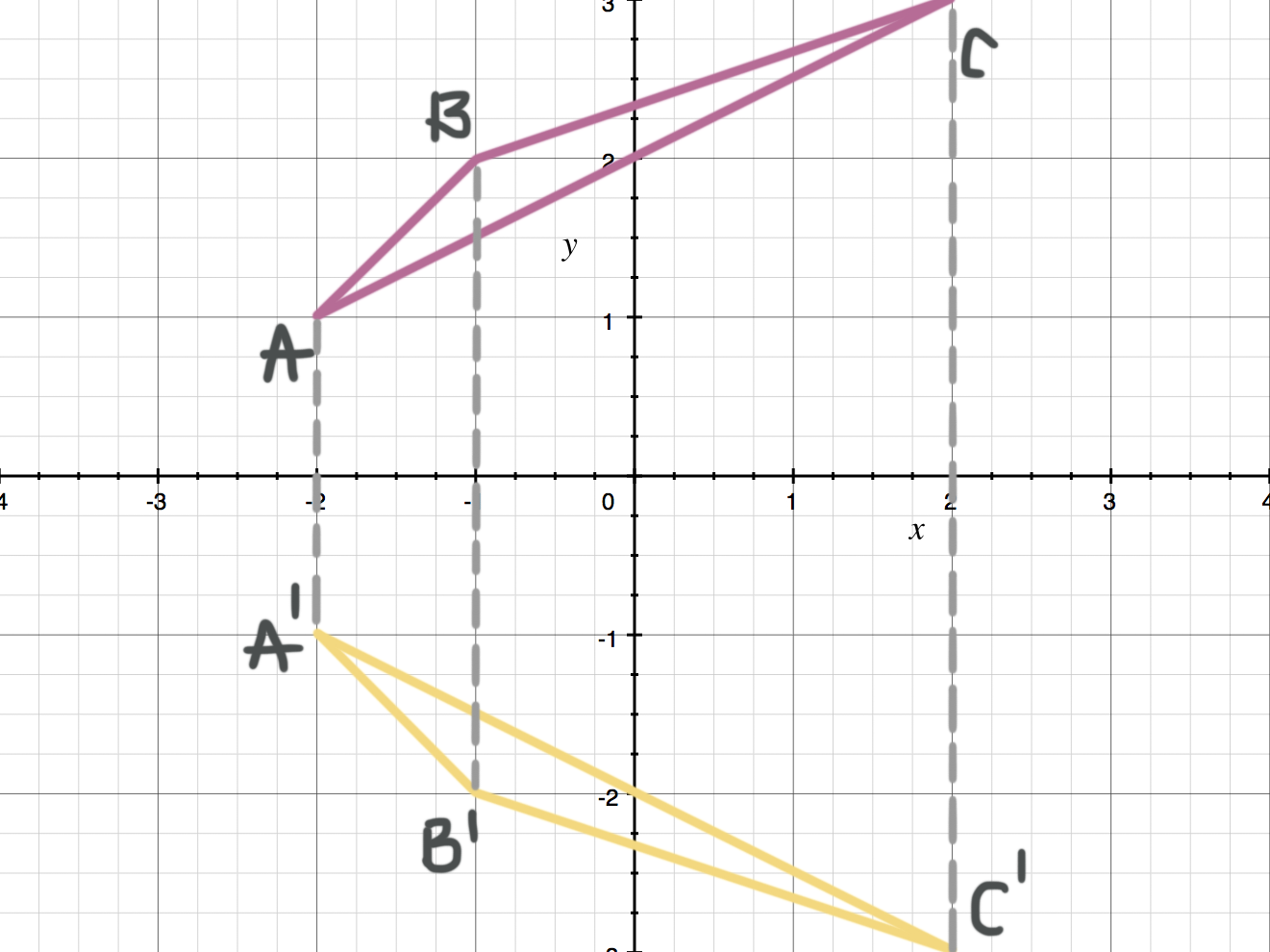
Reflecting In The Line Y X 2 Geogebra
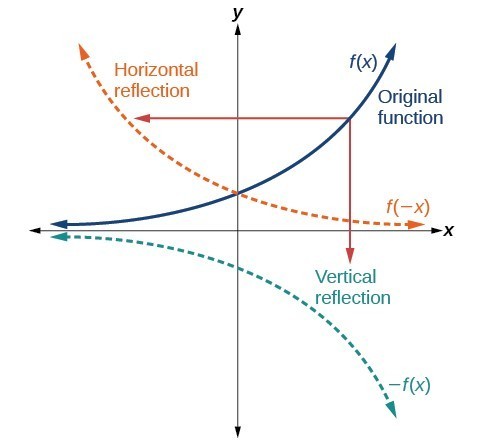



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




Reflection



Reflection Over Y Mx B Geogebra




Solved Consider The Function F X This Is A One To One Chegg Com



Algebraic Representations Of Reflections



Transformation Reflection Over X Axis




Reflection Over The Line Y X Math Showme




Reflection Transformation Matrix




Reflections Through The Axes And The Lines Y X And Y X Geogebra




Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Desmos Accessibility




Reflection Mathbitsnotebook A1 Ccss Math




Reflection Over The Line Y X Geogebra




Reflection Transformation Matrix
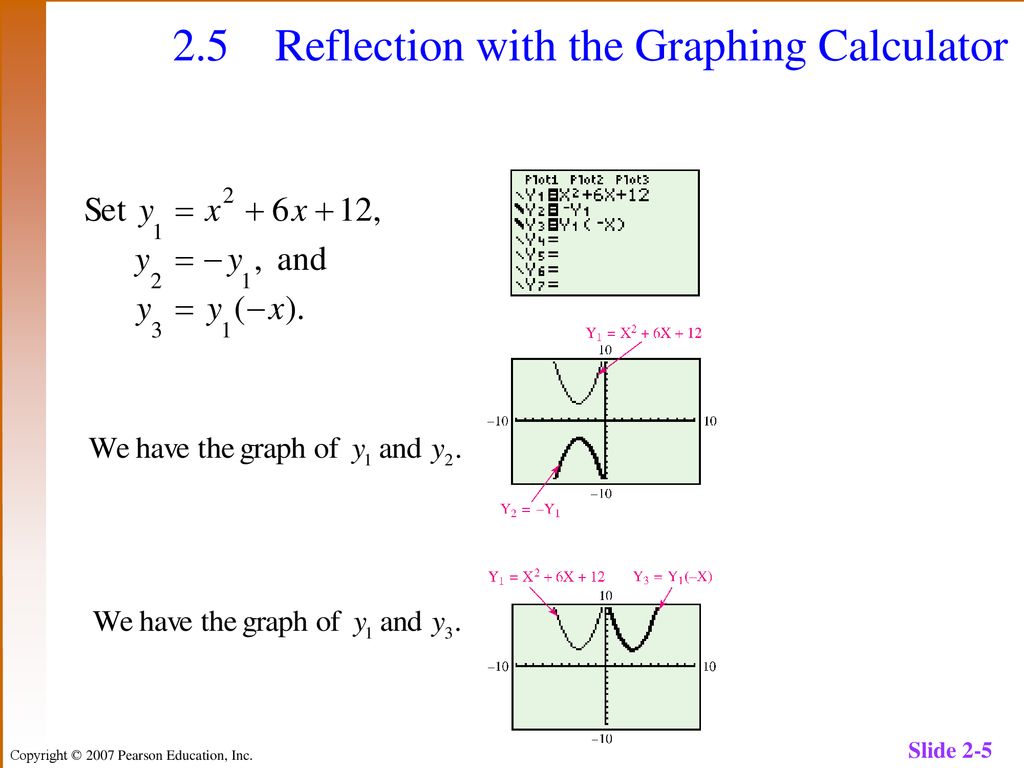



2 5 Stretching Shrinking And Reflecting Graphs Ppt Download
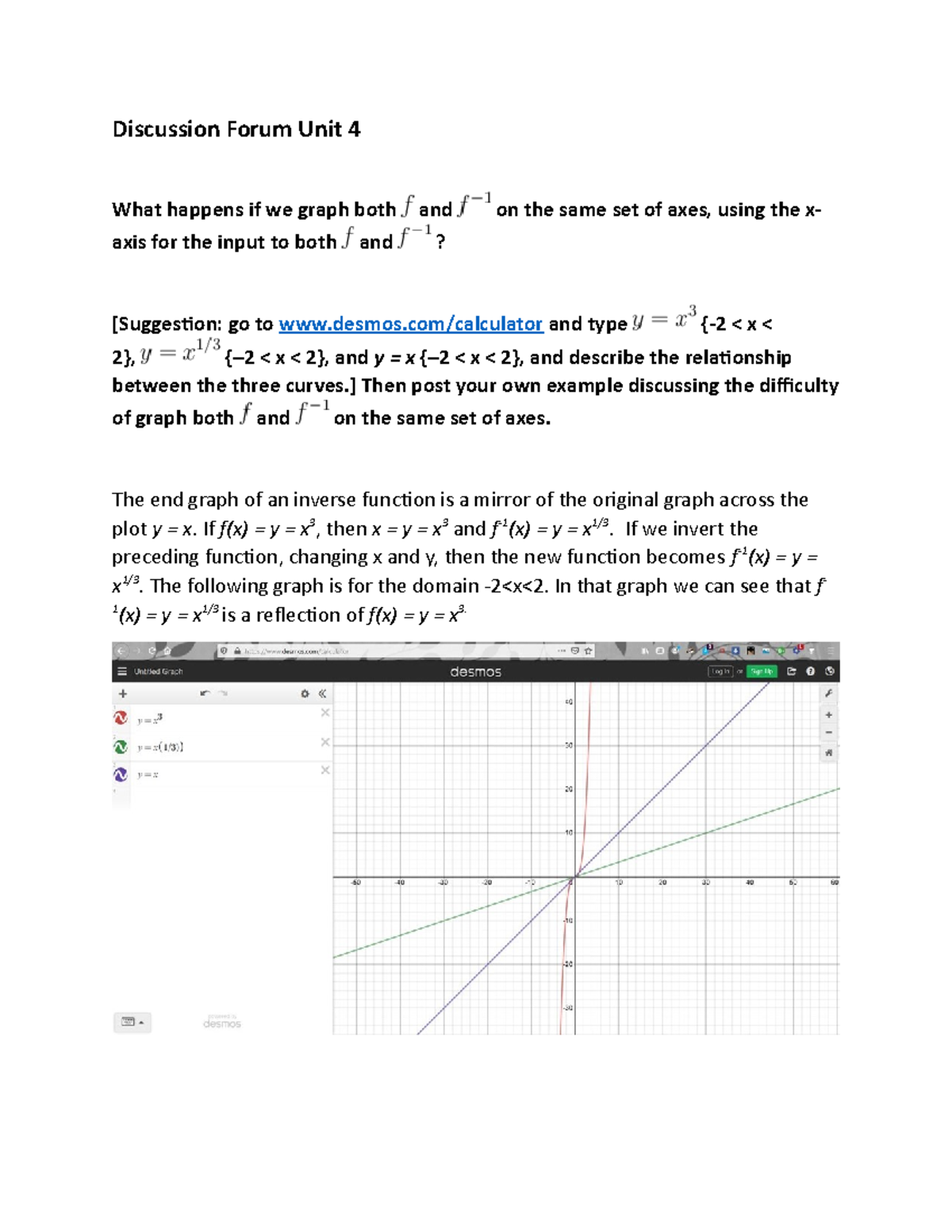



Discussion Forum Unit 4 Desmos Com Calculator And Type 2 Lt X Lt 2 2 Lt X Lt 2 And Studocu




Reflection Over The Y X Line Youtube



Reflection Across A Line Geogebra
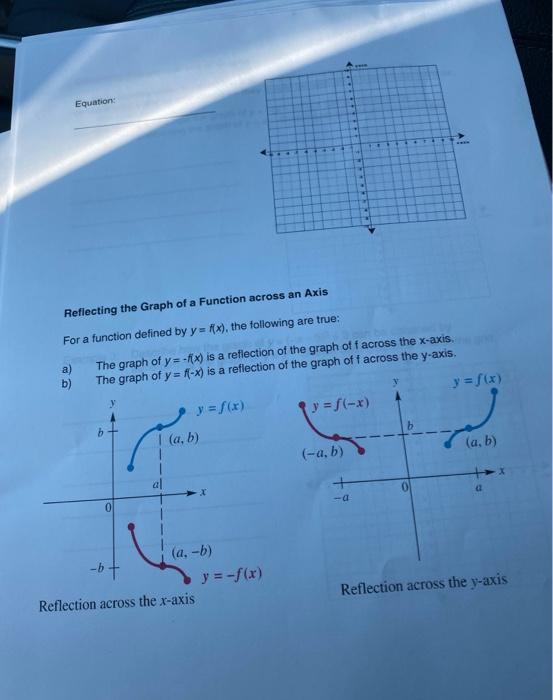



Solved Name Section 2 3 Reflecting Graphs Reflecting Across Chegg Com



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



1
.png)



Axis Of Symmetry Calculator With Steps Formula Equation
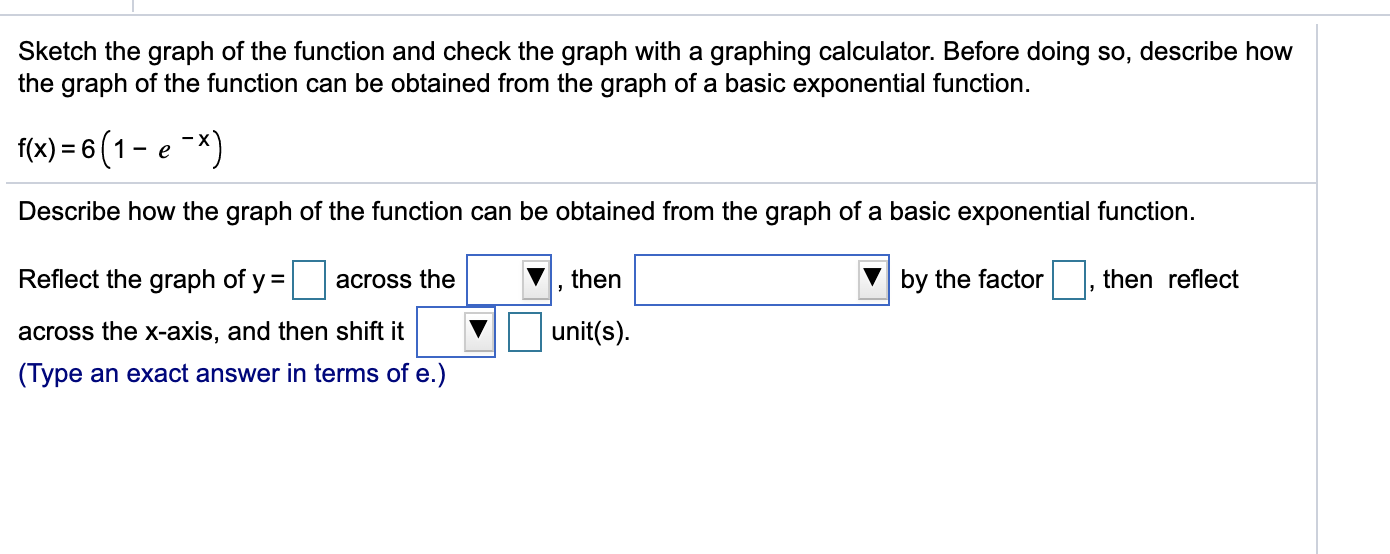



Solved Sketch The Graph Of The Function And Check The Graph Chegg Com




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
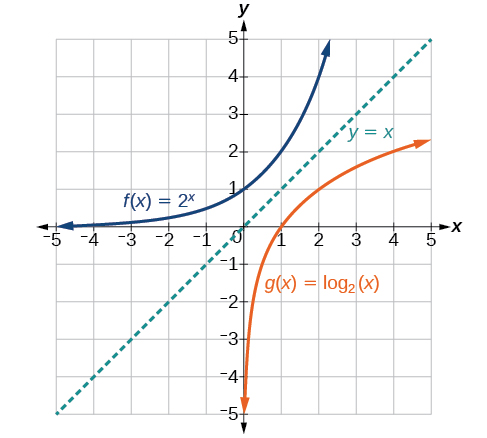



Graphs Of Logarithmic Functions Algebra And Trigonometry



Math Alive Geometry 1



Reflection Over X Axis Geogebra
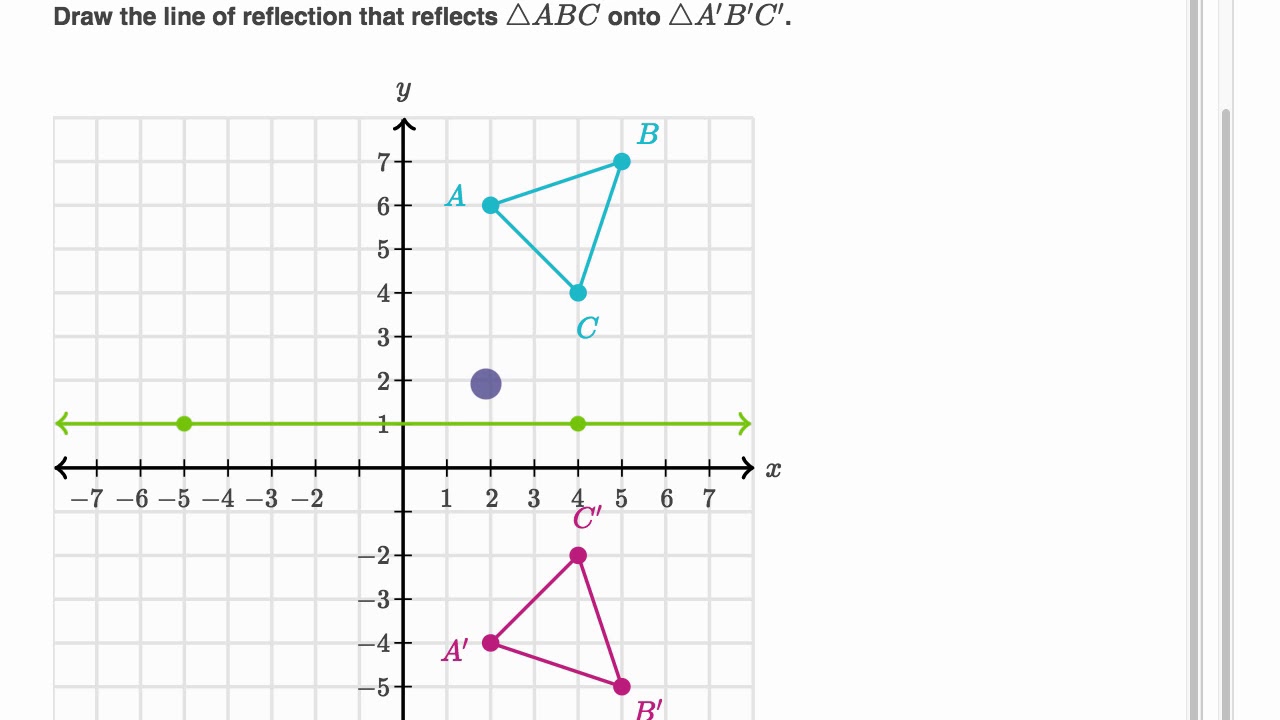



Line Of Reflection Example Youtube
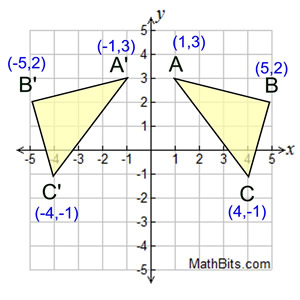



Reflection Mathbitsnotebook Geo Ccss Math




Reflecting Functions Introduction Video Khan Academy




Reflection In The Line Y X Geogebra




Reflection Over Y X Math Geometry Showme
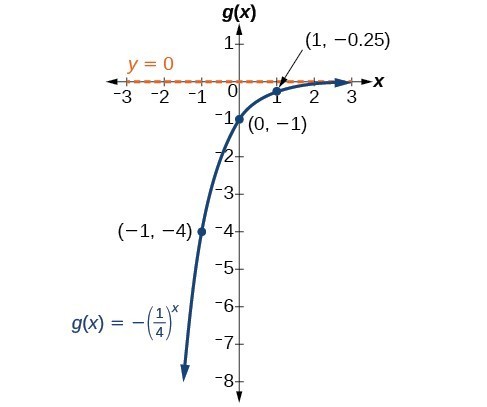



Graph Exponential Functions Using Transformations Math 1314 College Algebra



Solved Sketch The Graph Of The Function And Check The Graph With A Graphing Calculator Before Doing So Describe How The Graph Of The Function Ca Course Hero



0 件のコメント:
コメントを投稿