こうして求めた月の質量は、地球の質量の倍(123×102 倍)という憶えやすい値である。なお、地球の質量は598×10 24 kgである。この月の質量と、月の半径から求めた月の体積(半径rの球の体積は4πr 3 /3)から、月全体の平均密度を求めることができる。半径は剛性が剛心から平均的にどのくらい離れ ているかを示すものですから,剛心から柱まで の距離に一致しています。 もっとも単純な配置である4本柱が正方形の頂 点にあり,すべてX方向もY方向も剛性が1で ある階の弾力半径を求めてみましょう。 2= 2n3 2n1 = 3 n 2 1 n → 1 ですから、y の級数として収束半径は1です。従ってxの級数としても
Q Tbn And9gcqyrslclwl4zjqsiu Eb80r3ccsntxpibvziibi Muwysoknwz Usqp Cau
半径 求め 方
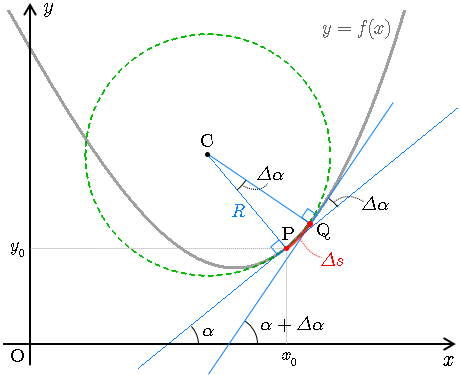
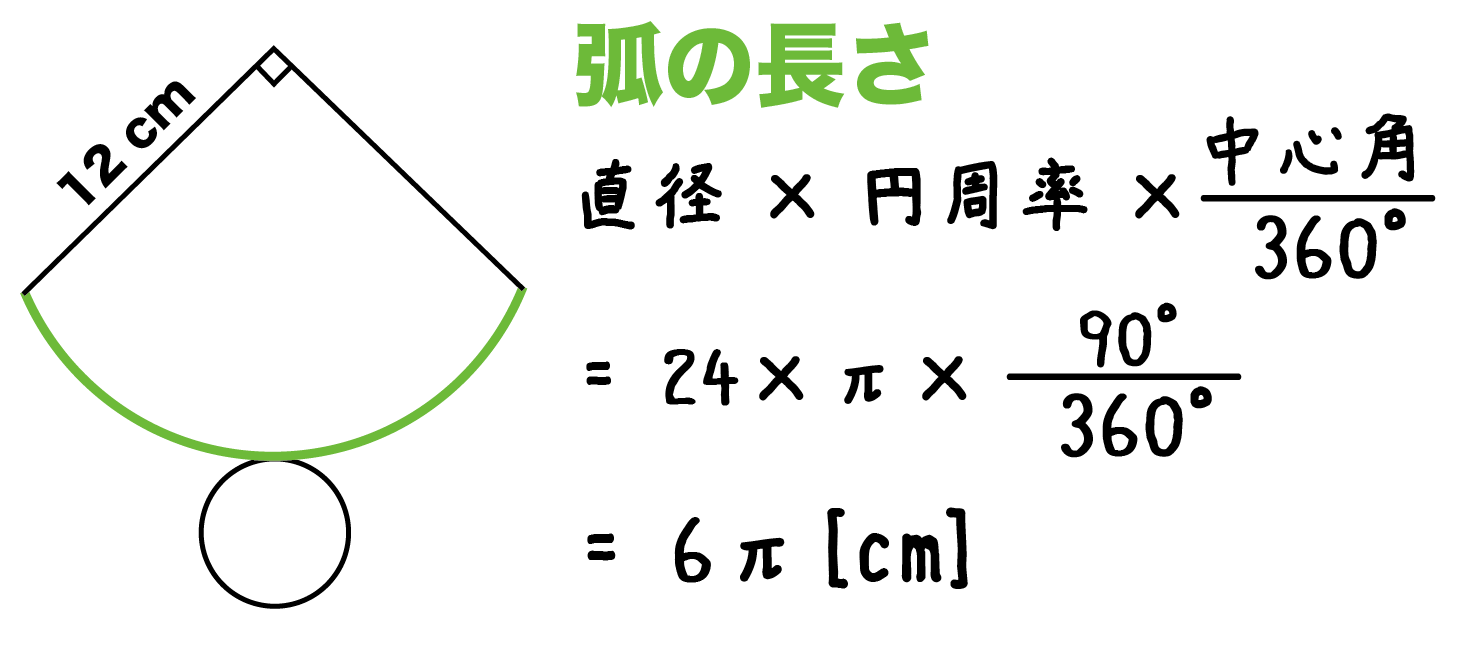
半径 求め 方-Xy x y 平面で定義された曲線 y = f(x) y = f (x) 上の点 P (x0, y0) (x 0, y 0) から曲線に沿って Δs Δ s だけ変位した点を Q とする.この Δs Δ s 部分を円弧とみなし,その円の中心を点 C ,角PCQを Δα Δ α とすると,この円の半径は半径をxとして、方程式を作って解く! 弧の長さが与えられているので 弧の長さの公式に x 、数を当てはめていきましょう。 (半径を公式通り r として計算してもOKだからね) すると、このような方程式ができあがります。 あとは、この方程式を解いて x の値を求めれば終わりです! 両辺をπで割って、消しちゃいましょう。 両辺に3を掛けて分数を消します




C 曲率半径を求めたいが 計算式がわからなかったので他の計算方法で求めたいです Teratail
曲率・曲率半径の感覚的な意味と求め方 レベル ★ 最難関大受験対策 極限,微分 更新日時 曲率半径 とは,曲線を「局所的に円の弧」とみなしたときの円の半径。 曲率 とは,曲率半径の逆数。 曲率・曲率半径について解説します。 曲率半径球の体積の求め方 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を代入して作業半径揚程図の見方移動式クレーンの辞典 手順1 図面または現地調査で、左図のように距離と高さを調べてください。 ① 旋回中心から 最初の障害までの距離と高さ ②次の障害があれば、そこまでの距離 ③荷を降ろしたり揚げたりする場所までの
円周率 π )という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 例題②半径 5 cmの円の面積を求めて下さい半径3cm、高さ10cmの円柱の表面積を求めなさい。 つぎの3ステップで求めることができるんだ。 Step1 底面の面積を求める! 円柱の底面積をもとめてみよう。 円柱の底面は「円」。 よって、底面積の求め方は、 半径×半径×円周率 になるよね!注意 原子半径 (Atomic Radii) 以下から引用 E Clementi, D L Raimondi, W P Reinhardt (1963) J Chem Phys 3686 イオン半径 (Ionic Radii) これらのデータは、イオン構造中で陽イオンと陰イオンを表すのに適した経験的なイオン半径を採用しています。イオン結晶、金属結晶、共有結合結晶、高分子など10あまりの
方が、かえって系外惑星の半径が大きく算出され、これは系外惑星の大気による散乱の 実半径を求めた。その結果、TrES1bは12木星半径(文献値は1099木星半径)、HATP43b は16木星半径(文献値は12木星半径)という値が求まった。こうしてエラトステネスは地球の大きさを測ったのです.もちろんその値は近似的なものでしかありませんでした.現在知られている地球の半径は約 6360 kmです. (注)地球は太陽の周りを一年かけて一周します.その軌道面に対して地球の自転軸は 235 °傾いています(図4).従って北半球が007 = 35 と算出します。 逆に下図のように、vcl=35のほうが先に決まっていて、その半径rを求めたい場合は、 式②を用いて、
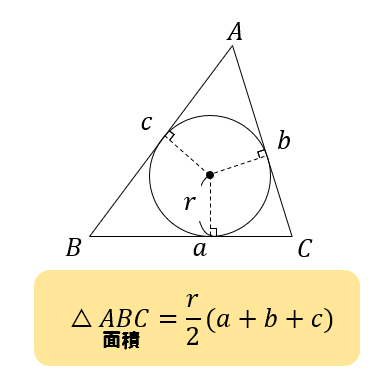



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方
これは大事な公式ですからしっかりと覚えておきましょう。 円の面積の求め方は、 (円の面積) = (半径) ×収束半径 は次のように求められる.(前述の例32と類似) のとき収束するから, すなわち, , になり,この級数は任意の実数 に対して収束する.なお、シュヴァルツシルトは、シュワルツシルト半径を曲率が無限大になる半径として求めたが、実際にはこれは座標の取り方による一種のメトリックであり、曲率が無限大になるのは r = 0 の特異点で




平面線形 曲線半径 と 曲線長 が分かっている時の交角8の出し方 道路設計 Com




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
の収束半径をy のべき級数として求めてやってあとでxに変換する方向で考えましょう。 y のべき級数としてのn 次の項の係数をa n と書けば Ø収束半径の求め方の一つであるダランベールの判定法を紹介します。 ダランベールの判定法 lim n → ∞ ∣ a n 1 a n ∣ = C4.補足向心力について 運動方程式より、上記の物体にはたらく、円の中心に向かう力Fは F = m・a = m・vω ①である。 ここで、 物体が円周上を1周するのにかかる時間を Ts とする。 すると、v・T = 2πr である。 また※1より、ω = 2π / T である。 この2つの式からπとTを消去




中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円の面積 算数用語集
星の半径を太陽半径との比の形で求めようとすれば、実際の計算はいくぶん簡 単になります。 L s を太陽の光度、Lを測りたい星の光度、T s を太 陽の温度、Tをその星の温度、R s を太陽の半径、そしてRをその星の半径と しましょう。 光度の比は次のように表すことができます。 L/L s = (4 p R 2 s T 4 )/ (4 p R s 2 s T s 4) = (R/R s) 2 (T/T s) 4 比R/R s について解くと、次の式を得直径=半径×2なので 半径×2=円周÷円周率 半径=円周÷円周率÷2 です!弧長(円弧の長さ)L、弦長d、矢高(円弧の高さ)h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると(空白にはしないでください)、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン法で計算しています。 ※180°以上の中心角の場合、および2つ解がある場合にも対応しました。 動かない




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




小学生でもできる円周率の求め方 いろいろな方法を紹介 数学の面白いこと 役に立つことをまとめたサイト
扇形の半径の求め方 扇形の半径を求めるときも、面積の公式または弧の長さの公式を利用します。 公式にわかっている値を代入して、「 \(\text{(半径)} = \) 〜 」の形に書き換えていけばいいだけです! 実際に例題を見てみましょう。円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 円の面積は、 「半径 ×上図は「半径r=500の縦断曲線を設置したい場合の縦断曲線長vclはいくつか」を考えていますので、 式①を用いて、 vcl = 500 ×




小6 算数 小6 旧 円の面積 Youtube



車の数学 26 車の運転と最小回転半径 計算式
太陽の質量も、月の質量の求め方と同様にケプラーの第3法則を用いて求める。こうして求められた太陽の質量は、19×10 30 kg(約×10 30 kg)である。地球の質量が5974×10 24 kgなので、太陽の質量は地球の質量の33万倍ということになる。D = ケーブルの公称外径 (単位 mm) ※1 引張などの負荷がかからない状態での可動 ※2 持ち運びや移動する設備で内部配線される場合の固定使用 ※3 L型屈曲試験のように錘などの負荷がかかる場合 ※4 ガントレークレーンなどでのカーテン状の使用 ※5 巻き取りドラムでの使用 ※6 移動する滑車に触れている部分 ケーブルベアでの使用の場合、最小曲げ半径は外径円周の求め方 公式と計算例 円周の長さを求める公式は、次の通りです。 l = πd = 2πr l = π d = 2 π r 直径d、半径 r の円 ここで、l は円周の長さ、π は円周率、d は円の直径、r は円の半径を表します。 小学生向けに、文字を使わずに書くと次のようになり




円錐の表面積の求め方 公式と計算例




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
A n a n1 Ø赤道半径の実測値の最良とされている推定値は、±01 m となります。 ただ、地球の半径には、赤道半径以外にも「極半径」と呼ばれるものがあります。地球の極半径は、約kmあり、赤道半径の方が極半径よりも約214kmほど大きくなります。(円周率π) ですね。 ここまでわかれば、準備完了です。 ・底面の円の面積は 3×3×π=9π㎡ ・高さは 8cm よって、求める円柱の




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



外接円とは 半径の公式や求め方 性質 書き方 受験辞典
車の数学(): 車の運転と最小回転半径(JavaScript版) 最小回転半径(Minimum turning radius)とはステアリング(ハンドル)を一杯に切って旋回したときに、外側前輪の接地面の中心が描く半径をいいます。小型乗用車の最小回転半径は概ね4~5m程度です。求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成します。 あとは、これを解いていけば の値(半径)を求めることができます。 この直径と半径 求め方 体積と直径の求め方 解らないので回答の仕方を教えてください。 ダイヤモンドの比重は351、炭素の原子量は1です。 原子1個当たりの体積と、原子を球と仮定したときの直径がわかりません。 よろしくお願いします



曲率半径




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
Http//wwwmathsisfuncom/definitions/radiushtml 半径を最も簡単に求める方法は直径を2で割ることです。直径がわからなくても、円周(C = 2\pi r )や円の面積(A = \pi r^{2} )など他の値が与えられこの点と中心間の距離を計算することで、半径を求められます。 公式d = √ ( (x2 x1)2 (y2 y1)2 (z2 z1)2)を使って半径を求めましょう。 球の中心と表面の1点の座標がわかっているので、この2点間の距離を計算すれば半径Z \ne a z = a で発散するとき,収束半径は r = 0 r= 0 r = 0 と定め,すべての z z z で収束するときは収束半径は r = ∞ r=\infty r = ∞ と規定する。 a = 0, x ∈ R a=0, x\in \mathbb {R} a = 0,x ∈ R とすると,最初の定義に一致しますね。
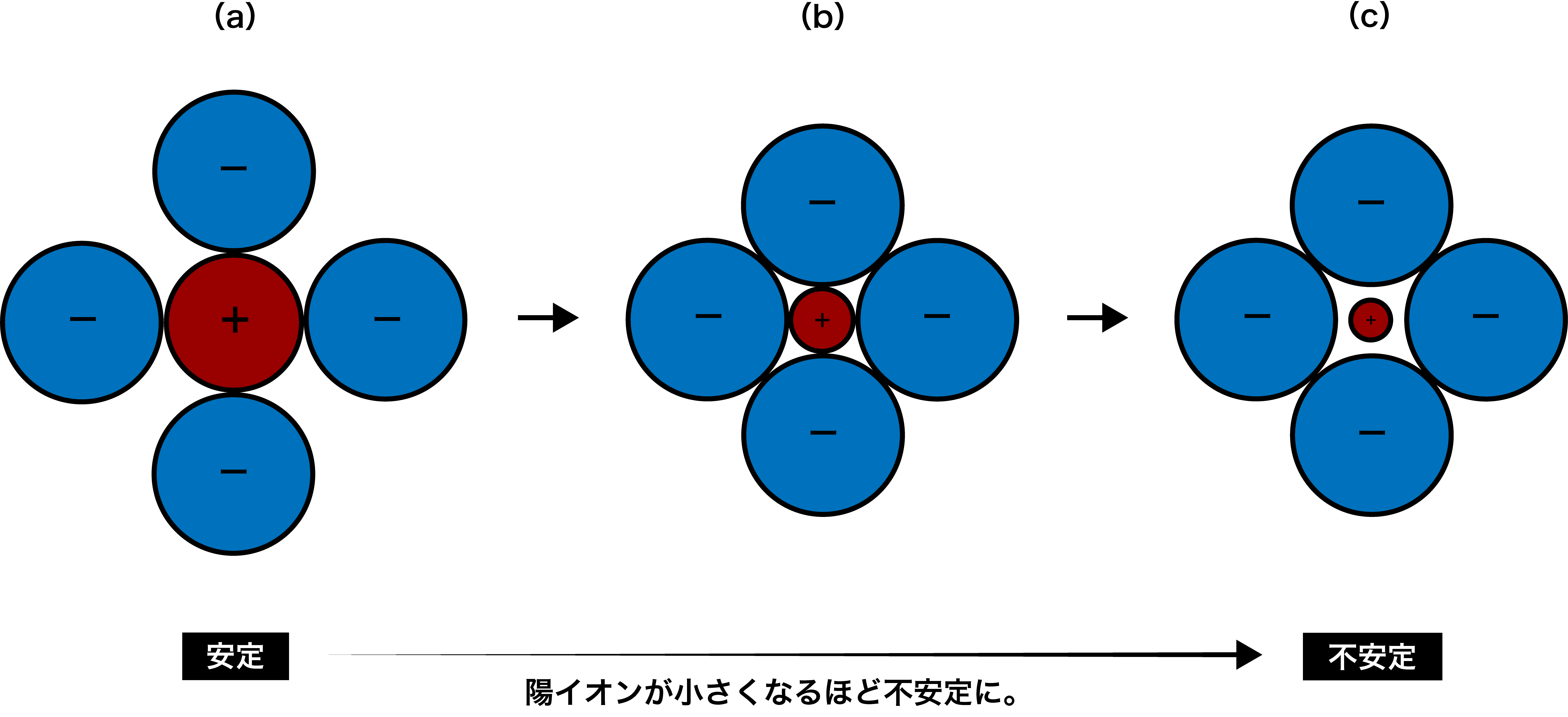



限界イオン半径比 定義 求め方 配位数との関係など 化学のグルメ




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
求まるとしたらどうやって求めているのでしょうか? 1 天文単位は最初 CFGauss さんによって地球太陽間の平均距離,より正確には地球の軌道長半径として定義されました. 軌道長半径は ケプラーの第三法則 を使って求めることができます.イオン結晶の限界イオン半径比の範囲外になると、そのイオン結晶は不安定となり、 配位数の異なる違う結晶構造に変化 する。 このように、温度や圧力の変化により、結晶構造が変化する現象を 相転移 という。 限界イオン半径比の求め方円の面積から半径 エンクロージャーに複数の円形ダクトを入れる際の面積から逆算して直径を割り出すために使用しました。 とても役に立ちました。 有難うございました。 数式に表記されいる 直径=area は間違いかと. 直径は英語で Diamater ご指摘ありがとうございます。 表記ミスを修正しました。 面積を入力してエンターキーを押すと計算結果が出るように




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト



世界一やさしい 円周率と 円周を求める問題の解き方 働きアリ




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ




Fichier 面心立方格子の原子半径の求め方 Svg Wikipedia




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
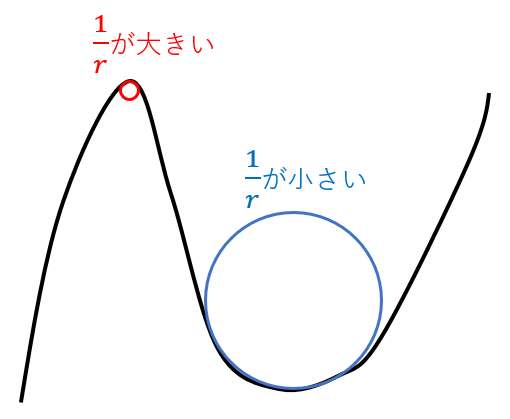



曲率と曲率半径のの求め方




C 曲率半径を求めたいが 計算式がわからなかったので他の計算方法で求めたいです Teratail
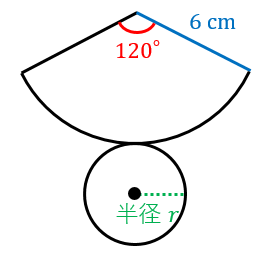



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




円の面積の求め方を自主学習ノートで復習しましょう 円の面積の基本的な練習問題 円の面積の求め方を確認しておき 学習ノート 学習 数学ノート



1




円周 円の面積の求め方 チーム エン




どんな物もブラックホールになり得る シュバルツシルト半径 を理系ライターが初心者目線で解説 ページ 3 4 Study Z ドラゴン桜と学ぶwebマガジン




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




小3 円 円の半径と直径 日本語版 Youtube




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
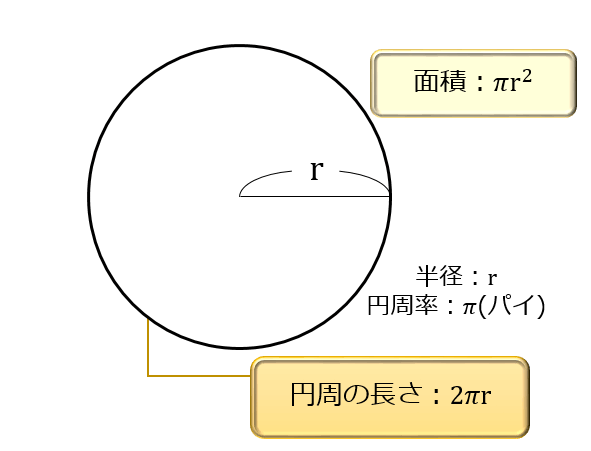



円周の求め方 円周率とは何か なぜ無限に続くのかを説明 その割り切れない理由について アタリマエ




円周の求め方 公式と計算例



半径の測定 測量



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典



収束半径の求め方を教えてください 画像の問題の解き方を教えてく Yahoo 知恵袋




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




地球の概観と構造 エラトステネスの方法について 地学基礎 定期テスト対策サイト
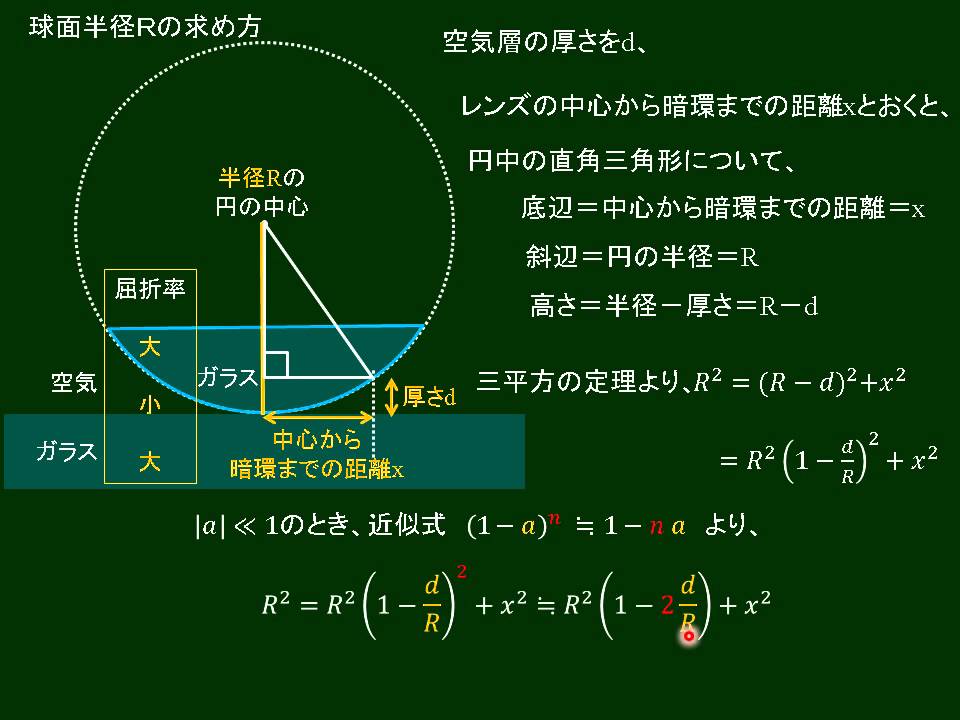



高校物理 ニュートンリングによる球面半径の求め方 Youtube
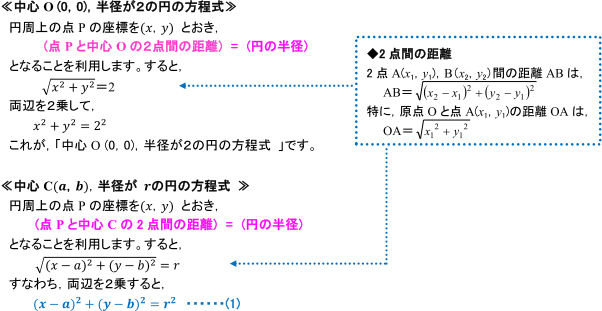



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座
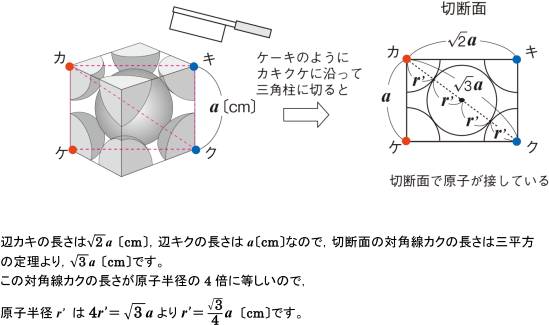



固体の構造と状態変化 単位格子の原子半径の求め方がわかりません 化学 定期テスト対策サイト



半径とrの関係は 1分でわかる単位の意味 記号 求め方 直径 D Fとの違い




曲率半径 曲線の曲がり具合を円で近似する話 すうがくブログ 式変形ch




円の面積の求め方 公式と計算例




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




分からないので式と答えお願いします Clear




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ




半径の計算方法を教えてください 弦長360 矢高10 半径は よろし 数学 教えて Goo




球の半径を求める 3つの方法 Wikihow




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun




車の 最小回転半径 くるくら




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




自動車開発 製作セミナー Chapter6 6 Youtube



円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ
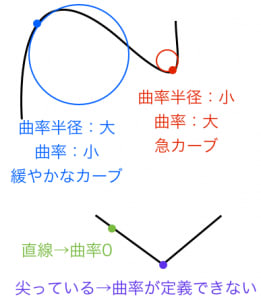



曲率 曲率半径の感覚的な意味と求め方 高校数学の美しい物語



Q Tbn And9gcqyrslclwl4zjqsiu Eb80r3ccsntxpibvziibi Muwysoknwz Usqp Cau



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




扇形の面積の求め方 公式と計算例




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



半径の求め方は 1分でわかる方法 公式 円周との関係 扇形の円弧から半径を求める方法
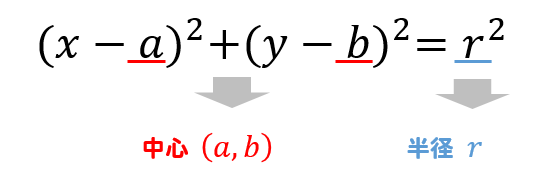



円の方程式 中心の座標と半径の求め方を解説 数スタ



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




小学校6年 円の面積の求め方 どうして半径 半径 3 14なの ふるやまんのマスラボ奮闘記
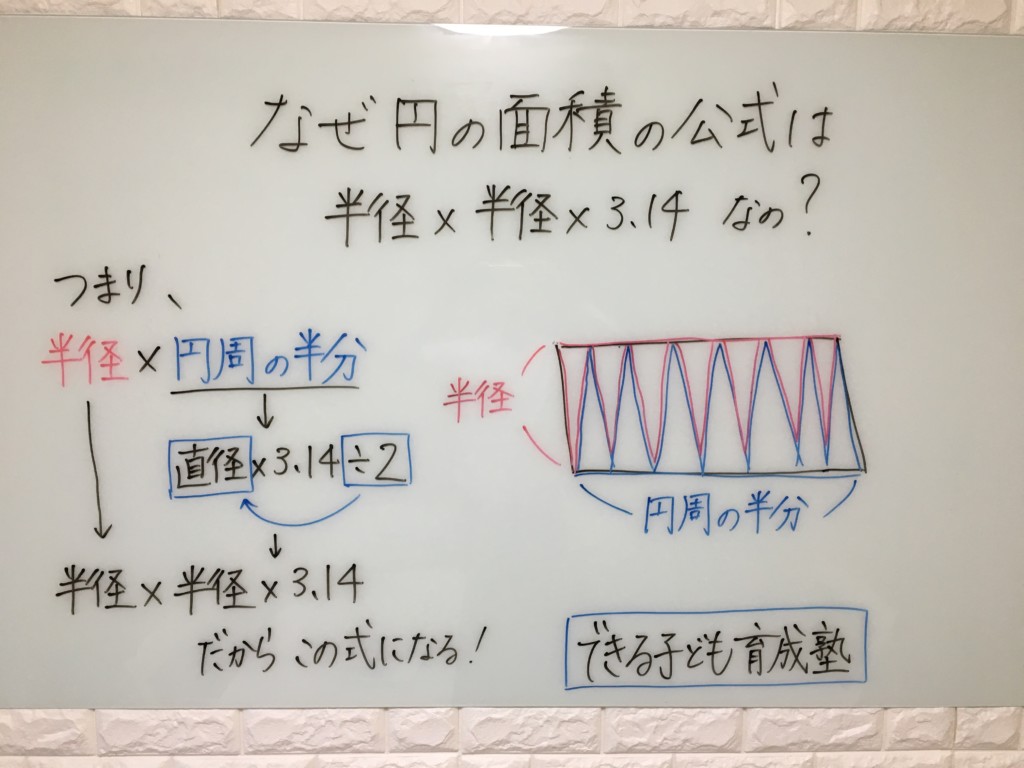



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




外接円の半径の求め方 Menkarm World




3分で分かる 三角形の外接円の半径の長さの求め方をわかりやすく 合格サプリ



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典




おうぎ形 半径の求め方をイチから解説 Youtube




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト



円の弧 弦の長さで円の半径を求める式をご教示ください 図の弧 弦の Yahoo 知恵袋



家具製作資料 半径の判らない円弧半径の求め方 家具制作鯛工房




円周の求め方と円の面積について アタリマエ
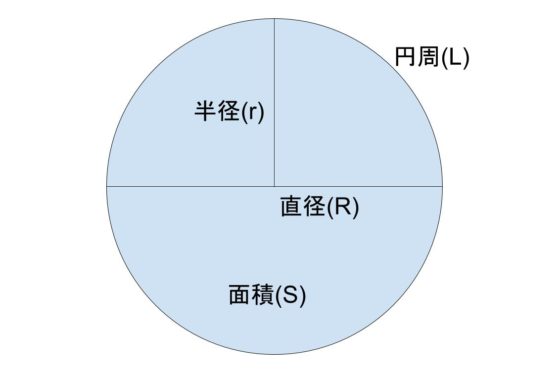



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ
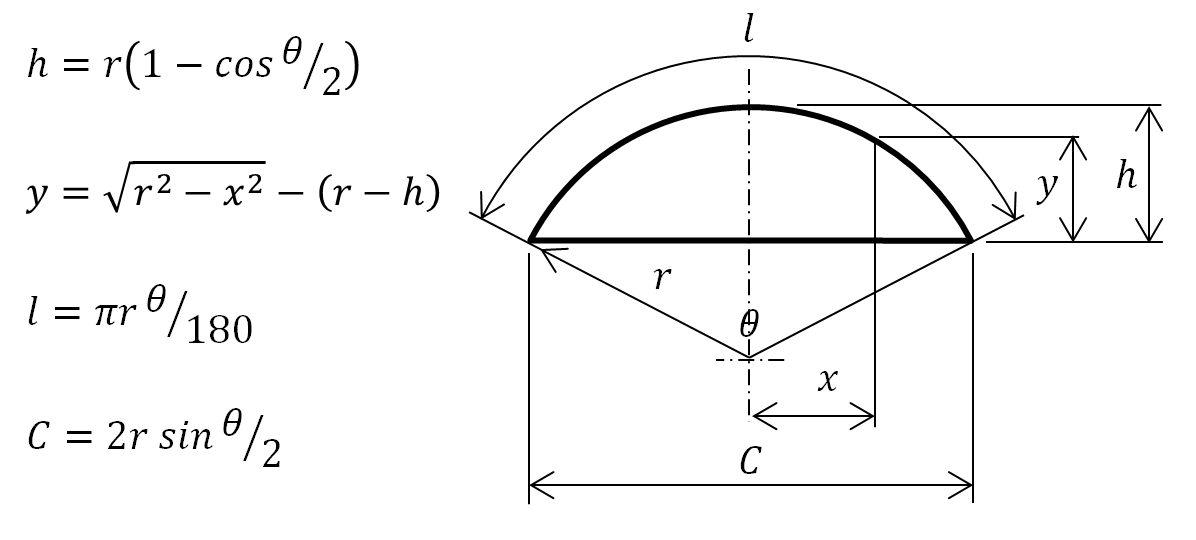



円弧高さ 円弧長さ 円弧長さ 円弧幅の計算 1 高精度計算サイト




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




Fichier 体心立方格子の原子半径の求め方 Svg Wikipedia



中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題



曲率と曲率半径




Fichier 面心立方格子の原子半径の求め方 Svg Wikipedia




高校数学 内接円の半径の求め方 例題編 映像授業のtry It トライイット




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
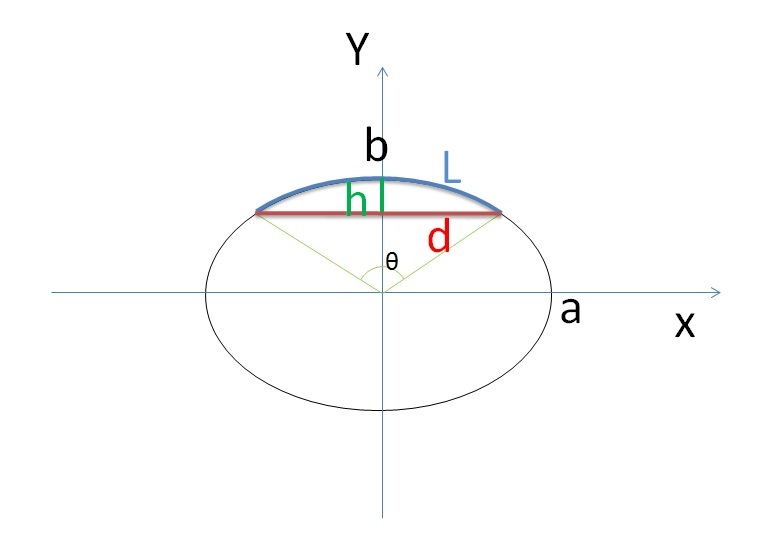



楕円の円弧 弦長 矢高を長軸半径 短軸半径 中心角から求める 高精度計算サイト



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau




円錐の表面積の求め方 You Look Too Cool




半円や4分の1の円 四分円 の面積を計算する方法 モッカイ




公式を図解 すい体の体積 円すいの表面積の求め方
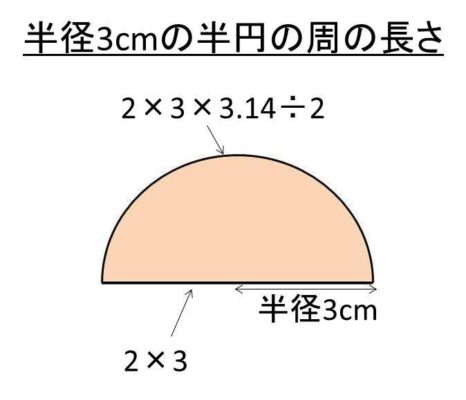



半円の周の長さの計算方法 モッカイ




おうぎ形 半径の求め方 数学の記録



0 件のコメント:
コメントを投稿